
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ускорение МТ
|
|
|
|
Понятно, что скорость также меняется во времени. Пример - разгон авто.
Введем характеристику, описывающую скорость изменения скорости (временное изменение).
Для этого рассмотрим отрезок траектории между двумя соседними точками М1 и М2, которые занимала МТ. В каждой точке  направлен по касательной к этой траектории.
направлен по касательной к этой траектории.
Введем разные векторы  1 и
1 и  2 по формуле D
2 по формуле D  =
=  2-
2-  1 (1).
1 (1).
▼ По определению вектор равный W =  (2) (W=vj) называется вектором среднего ускорения за время Dt. Далее поступаем также как и с определением мгновенной скорости. Мгновенное ускорение МТ определяется как предел среднего ускорения (2)
(2) (W=vj) называется вектором среднего ускорения за время Dt. Далее поступаем также как и с определением мгновенной скорости. Мгновенное ускорение МТ определяется как предел среднего ускорения (2)  =
= 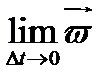 ср=
ср=  (3) если этот предел существует.
(3) если этот предел существует.
▼ Мгновенное ускорение определяется  =
= 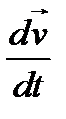 (4).
(4).
 =
=  ,
,  =
= 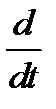 (
( ) (5).
) (5).
▼ Выражение (5) обозначает вторую производную по времени от 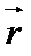 (производная от первой производной).
(производная от первой производной).  =
=  (6).
(6).
Разобьем D  =D
=D  n+D
n+D  τ (8) по построению (М1В=
τ (8) по построению (М1В=  ), отвечает за удлинение вектора скорости МТ в процессе ее движения, а D
), отвечает за удлинение вектора скорости МТ в процессе ее движения, а D  n отвечает за поворот D
n отвечает за поворот D  в процессе движения МТ. Представим (8) в виде (3):
в процессе движения МТ. Представим (8) в виде (3):  =
=  n+
n+  τ (9);
τ (9);  n =
n = 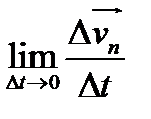 (10);
(10);  τ=
τ= 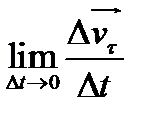 (11);
(11);  τ=
τ= 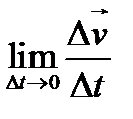 =
=  (12).
(12).
▼  τ по величине характеризует быстроту изменения величины скорости и очевидно, при Dt→0 сам
τ по величине характеризует быстроту изменения величины скорости и очевидно, при Dt→0 сам  τ будет направлен по направлению скорости в этой точке, т.е. по касательной, по этой причине
τ будет направлен по направлению скорости в этой точке, т.е. по касательной, по этой причине  τ называется касательным или тангенсальным ускорением МТ. Рассмотрим И2, рассмотрим равнобедренный треугольник МАВ, Dα+2β=
τ называется касательным или тангенсальным ускорением МТ. Рассмотрим И2, рассмотрим равнобедренный треугольник МАВ, Dα+2β=  (13).
(13).
▼  n – направленно
n – направленно  - но к вектору
- но к вектору  .
.
( ,
,  ,
,  ) (14).
) (14).
Проведем в М1 и М2 перпендикуляры к касательным. Они пересекаются в точке О.
Для малых Dt, М1О  М2О=R (15).
М2О=R (15).
Рассмотрим DМ1М2О. R  /
/ 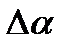 (17), R=
(17), R=  (18).
(18).
▼ Величина определяемая по формуле (18) называется радиусом кривизны траектории.
Рассмотрим DМ1М2О и DМ1АВ (они подобны).  - величина перемещения (19).
- величина перемещения (19).
 =>
=>  (20).
(20).
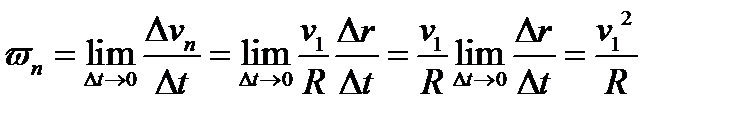 .
.
Мы доказали 
 (21).
(21).
▼  n –величина которая определяется формулой (21) и которая направлена перпендикулярно к касательной к траектории называется нормальным вектором ускорения.
n –величина которая определяется формулой (21) и которая направлена перпендикулярно к касательной к траектории называется нормальным вектором ускорения.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 642; Нарушение авторских прав?; Мы поможем в написании вашей работы!