Линейные нормированные пространства

Определение нормированного пространства. Примеры.

Нормированным векторным пространством называется векторное пространство с заданной на нем нормой.

Норма — функционал, заданный на векторном пространстве и обобщающий понятие длины вектора или абсолютного значения числа.

Примеры:

Любое предгильбертово пространство можно считать нормированным, так как скалярное произведение порождает естественную норму

Гёльдеровы нормы 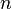-мерных векторов (семейство):,

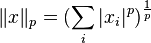
где (обычно подразумевается, что это натуральное число).

В частности:

(евклидова норма),

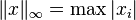(это предельный случай ).

Нормы функций в 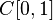— пространстве вещественных (или комплексных) непрерывных функций на отрезке [0,1]:

— в смысле этой нормы пространство 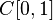непрерывных на отрезке функций образует полное линейное пространство. Этого нельзя сказать о следующих двух примерах нормы на этом пространстве, тем не менее, законных:

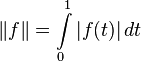
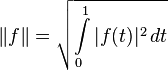
Аналогично можно ввести нормы для конечномерных векторных функций конечномерных векторных аргументов, заменив 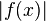на , а интегрирование по отрезку интегрированием по области (максимум же на отрезке — в соответствующем случае — максимумом на области).

Некоторые виды матричных норм.

Порожденные нормы:

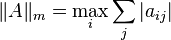
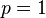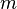: -норма,

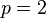(евклидова норма) и m = n (квадратные матрицы), подчиненная норма матрицы называется спектральная норма. Спектральная норма матрицы Aравна наибольшему сингулярному числу матрицы A или квадратному корню из наибольшего собственного числа положительно полуопределённой матрицы 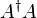: 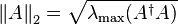, где 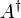обозначает матрицу, сопряжённую к матрице .

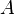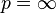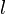: -норма

Здесь 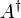— сопряжённая к 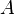матрица, 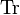— след матрицы.

Поэлементная 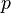-норма ():

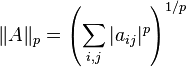
Норма Фробениуса:.

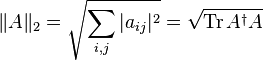
Дата добавления: 2015-04-24