Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона

Пусть имеем функцию 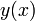, заданную в равноотстоящих точках отрезка 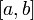с помощью

значений .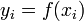

Для нахождения на 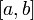производных 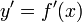, 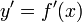и т. д. функцию приближенно заменим

интерполяционным полиномом Ньютона, построенным для системы узлов .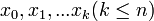

Имеем:

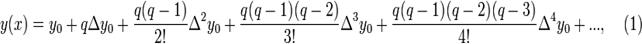
где 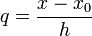и .

Производя перемножение биномов, получим:

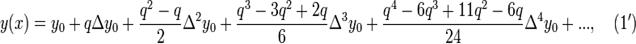
Так как

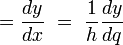
то

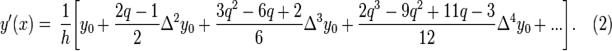
Аналогично, так как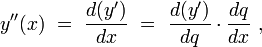

то

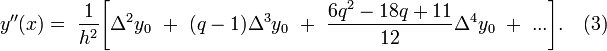
Таким же способом можно вычислить производные функции 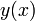любого порядка

При нахождении производных 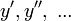в фиксированной точке 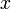в качестве 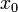выбирают ближайшие табличные значения аргумента.

В том случае, если необходимо найти производные функции 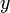в основных табличных точках 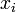, то полагают 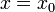, следовательно 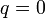и получают:

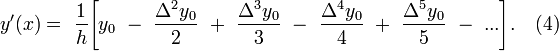
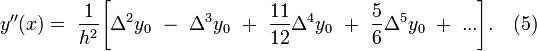
Формулы применяют, для начальных строк таблицы. Для последних строк таблицы используют формулы получающиеся при дифференцировании второй интерполяционной формулы Ньютона

Если 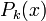- интерполяционный полином Ньютона, содержащий разност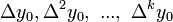и и

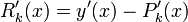
Известно что:

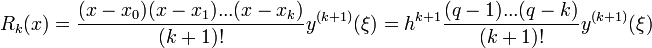
где ξ - некоторое промежуточное значение между узлами интерполирования 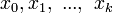и рассматриваемой

точной 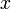. Поэтому, полагая, что 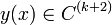, получим:

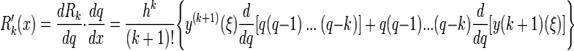
Отсюда при 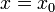и, следовательно, при 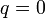и учитывая,

что 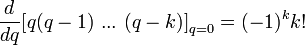?,будем иметь:

.

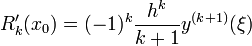Так как 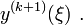во многих случаях трудно оценить, то при <\math>\ h</math> малом приближенно полагают:

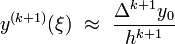
и, следовательно,

.

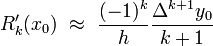Аналогично может быть найдена погрешность 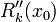для второй производной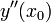

Дата добавления: 2015-04-24