Нормальное уравнение плоскости

Уравнение плоскости, проходящей через три данные точки

Пусть плоскость проходит через точк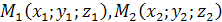и и 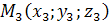, не лежащие на одной прямой и 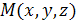– произвольная точка плоскости. Тогда векторы ,

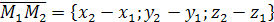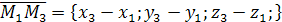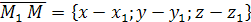, компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем:

.

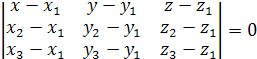Это уравнение, которому удовлетворяют координаты 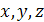любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.

Положение плоскости 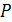вполне определяется заданием единичного вектора 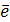, имеющего направление перпендикуляра 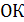, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра

Пусть 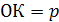, а 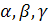– углы, образованные единичным вектором 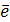с осям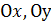и и 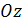; 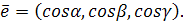Возьмем на плоскости произвольную точку 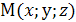и соединим ее с началом координат. Образуем вектор 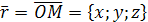. При любом положении точки Μ на плоскости 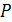проекция радиус-вектора 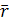на направление вектора 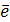всегда равно 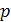: 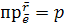, т.е. 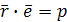или 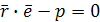– нормальное уравнение плоскости в векторной форме. Записав его в координатах получим нормальное уравнение плоскости в координатной форме:

.

Дата добавления: 2015-04-24