Понятия алгебраической операции, группоида, полугруппы и группы

Парабола, ее определение, уравнение.

Параболой (рис.1) называется геометрическое место точек, равноудалённых от заданной точки F, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

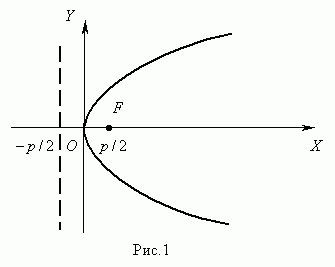
Уравнение параболы (рис.1):

y ² = 2 p x.

Здесь ось ОХ является осью симметрии параболы.

Пусть Р (х ₁, у ₁) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид:

у ₁ y = p (x + х ₁).

Условие касания прямой y = m x + k и параболы y ² = 2 p x:

2 m k = p.

Определение алгебраической операции. Соответствие, в силу которого каждой паре a, b элементов множества M, взятых в данном порядке, соответствует единственный третий элемент с того же множества M, называется алгебраической операцией, определенной в M.

Г руппоид (тоже самое что и магма, только термин группоид старше) - множество с одной бинарной операцией 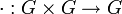, обычно называемой умножением. Помимо требования замкнутости множества относительно заданной на нём операции, других требований к операции и множеству не предъявляется.

Полугруппой называется всякое множество с заданной на нем бинарной ассоциативной операцией. Или это группоид с ассоциативной операцией. Пример: Положительные целые числа с операцией сложения. Любая группа является также и полугруппой.

Структура: Если , то принято обозначать

Группа — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам.

Примерами групп являются действительные числа с операцией сложения, множество вращений плоскости вокруг начала координат и т. п.

Определения. Непустое множество с заданной на нём бинарной операцией 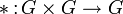называется группой 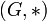, если выполнены следующие аксиомы:

1. ассоциативность: ;

2. наличие нейтрального элемента: ;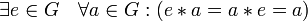

3. наличие обратного элемента: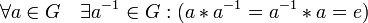

32. Определение кольца и поля. Простейшие свойства колец и полей.

Дата добавления: 2015-04-24