Вопрос № 2. Представление информации в цифровых автоматах

Вопрос №1

Представление информации в цифровых автоматах

Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

· даёт представления множества чисел (целых и/или вещественных);

· даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);

· отражает алгебраическую и арифметическую структуру чисел.

Системы счисления подразделяются на позиционные, непозиционные и смешанные.

История:

· Единичная система (черточки)

· Древнеегипетская непозиционная десятичная с/с (В древнеегипетской системе счисления, которая возникла во второй половине третьего тысячелетия до н.э., использовались специальные цифры для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из них повторялась не более девяти раз.)

· Вавилонская шестидесятиричная с/с (Числа в этой системе счисления составлялись из знаков двух видов: прямой клин служил для обозначения единиц, а лежачий клин - для обозначения десятков. Для определения значения числа надо было изображение числа разбить на разряды справа налево. Новый разряд начинался с появления прямого клина после лежачего, если рассматривать число справа налево)

· Римская с/с (Знакомая нам римская система не слишком принципиально отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, и 1000 используются заглавные латинские буквы I, V, X, C, D и M соответственно, являющиеся цифрами этой системы счисления.)

· Славянская с/с (Данная система счисления является алфавитной т.е. вместо цифр используются буквы алфавита. Данная система счисления применялась нашими предками и была достаточно сложной, т.к. использует в качестве цифр 27 букв)

· Греческая (Данная система счисления, так же как и славянская, является алфавитной, т.е. использует буквы в написании чисел. Определённой букве в соответствие ставилась цифра)

Позиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).

Целое число b > 1, называется основанием системы счисления. Система счисления с основанием b также называется b-ричной

Целое число x в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b:[1]

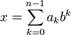, где — это целые числа, называемые цифрами, удовлетворяющие неравенству

Каждая степень 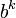в такой записи называется разрядом (позицией), старшинство разрядов и соответствующих им цифр определяется значением показателя степени k. Обычно для ненулевого числа x требуют, чтобы старшая цифра 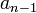в b-ричном представлении была также ненулевой.

Дата добавления: 2015-04-24