Вопрос № 18. (b,a) для которых существует (a,b)

Умножения

Обращения

Дополнения

Пересечения

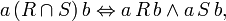
(b,a) для которых существует (a,b)

(a,b)×(b,c)=(a,c)

Бинарное отношение R на множестве X называется отношением порядка, или отношением частичного порядка, если имеют место

• Рефлексивность
• Транзитивность
• Антисимметричность

Множество X, на котором введено отношение частичного порядка, называется частично упорядоченным.

Отношение R, удовлетворяющее условиям рефлексивности, транзитивности, антисимметричности также называют нестрогим, или рефлексивным частичным порядком и обычно обозначают символом . Если условие рефлексивности заменить на условие антирефлексивности: 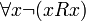, то получим определение строгого, или антирефлексивного частичного порядка, обозначаемое обычно символом <. В общем случае, если R — транзитивное, антисимметричное отношение, то

— рефлексивный порядок

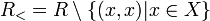— антирефлексивный порядок.

Отношение эквивалентности — двухместное отношение R между предметами х и у в предметной области D, удовлетворяющее следующим аксиомам (условиям):

• рефлексивности: xRx (предмет находится в отношении R к самому себе);
• симметричности: xRy yRx (если предмет х находится в отношении R к предмету у, то и у находится в отношении R к х);
• транзитивности: xRy&yRz = xRz (если предмет х находится в отношении R к предмету у и у находится в отношении R к z, то х находится в отношении R к г).

Таким образом, отношение типа равенства является одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, обмениваемость товаров на рынке, подобие, одновременность.

Дата добавления: 2015-04-24