Вопрос № 17

Вопрос № 16

Вопрос № 15

Вопрос № 14

Вопрос № 13

Бинарные отношения

Декартово (прямое) произведение множеств: Z:

X - 1-e исходное множество (состоит из элементов xi)

Y - 2-е исходное множество (состоит из элементов yj)

Z = X ⊗ Y - множество всех упорядоченных пар [ xi, yj ]

Пример:

X = { a, b, c}, Y = {1,2};

X ⊗ Y = {[a,1], [a,2], [b,1], [b,2], [c,1], [c,2]}.

Отношением R называется некоторое подмножество декартового произведения множеств: R ⊂ Z. Например: R = {a1, c2, a2}. Это двухместное отношение. Бинарное отношение – это двухместное отношение, в определении которого используется декартов квадрат, то есть Z = X ⊗ X (Y = X). Многоместным отношением R называется некоторое подмножество многократного декартового произведения множеств: R ⊂ Z.

z = [x1, x2, x3,..., xn-1, xn] - кортеж = «n – ка»: [a,1,x] – тройка, [a,1,x,M] – четверка, [y,3] – пара. Схема отношения: R (атрибут, атрибут,..., атрибут). Пример: Расписание (№ рейса, п.н., Т отпр.)

Рефлексивность - если всякий элемент этого множества находится в отношении R с самим собой

Антирефлексивность (иррефлексивность). - если всякий элемент этого множества ненаходится в отношении R с самим собой

Симметричность. - если для каждой пары элементов множества (a,b) выполнение отношения aRb влечёт выполнение отношения bRa.

Антисимметричность. - если для каждой пары элементов множества (a,b) выполнение отношения aRb влечёт невыполнение отношения bRa.

Транзитивность. - если для любых трёх элементов множества a,b,c выполнение отношений aRb и bRc влечёт выполнение отношения aRc.

Асимметричность. Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.

Операции над бинарными отношениями:

объединения,

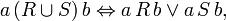
Дата добавления: 2015-04-24