Вопрос № 25. Пусть на множестве A = {1,2,3,4} задано отношение R = {(1,

Вопрос № 24

Вопрос № 23

Вопрос № 22

Формальные языки

Вопрос № 21

Вопрос № 20

Замыкания

Вопрос № 19

Пусть на множестве A = {1,2,3,4} задано отношение R = {(1,2),(3,4),(4,2)}. Видно, что отношение R не симметрично, не рефлексивно и не транзитивно. Замыканием R относительно свойства симметричности является R * = {(1,2),(3,4),(4,2);(2,1),(4,3),(2,4)}. Замыканием R относительно рефлексивности является R * = {(1,2),(3,4),(4,2);(1,1),(2,2),(3,3),(4,4)}. Замыканием R относительно транзитивности является множество R * = {(1,2),(3,4),(4,2);(3,2)}.

Форма́льная систе́ма (форма́льная тео́рия, аксиоматическая теория) — результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка, причем все условия, регулирующие употребление этих слов в теории, явно высказаны посредством аксиом и правил, позволяющих вывести одну фразу из других.

формальный язык — это множество конечных слов (строк, цепочек) над конечным алфавитом. Понятие языка чаще всего используется в теории автоматов, теории вычислимости и теории алгоритмов.

Формальный язык может быть определен по-разному, например:

Простым перечислением слов, входящих в данный язык. Этот способ, в основном, применим для определения конечных языков и языков простой структуры.

Словами, порождёнными некоторой формальной грамматикой (см. иерархия Хомского).

Словами, порождёнными регулярным выражением.

Словами, распознаваемыми некоторым конечным автоматом.

Если алфавит задан как {a, b}, а язык L включает в себя все слова над ним, то слово ababba принадлежит L. Пустое слово (то есть строка нулевой длины) допускается и часто обозначается как e, ε или Λ.

Некоторые примеры формальных языков:

множество всех слов над {a, b}

множество {an}, где n — неотрицательное число, а an означает, что a повторяется n раз

множество синтаксически корректных программ в данном языке программирования

Согласно Хомскому, формальные грамматики делятся на четыре типа. Для отнесения грамматики к тому или иному типу необходимо соответствие всех её правил (продукций) некоторым схемам.

Тип 0 — неограниченные

К типу 0 по классификации Хомского относятся неограниченные грамматики (также известные как грамматики с фразовой структурой). Это — все без исключения формальные грамматики. Для грамматики G(V_T,V_N,P, S), V=V_T∪V_N[1] все правила имеют вид:

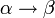, где α — любая цепочка, содержащая хотя бы один нетерминальный символ, а β — любая цепочка символов из алфавита.

Практического применения в силу своей сложности такие грамматики не имеют.

Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма. В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.

Дата добавления: 2015-04-24