Погрешность суммы и разности(вывод абсолютной и относительной погрешности из общих формул решения основной задачи теории погрешности)

Десятичная запись приближенного числа. Значащая цифра. Верные знаки числа(определение верных и значащих цифр, примеры; теория о связи относительной погрешности и числа верных знаков).

Верные знаки числа.

Определение. Значащей цифрой приближенного числа а называется всякая цифра, отличная от нуля, и нуль, если он расположен между значащими цифрами или является представителем сохраненного десятичного разряда.

Например, в числе 0,00507 = 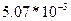имеем 3 значащие цифры, а в числе 0,005070= 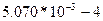значащие цифры, т.е. нуль справа, сохраняя десятичный разряд, является значащим.

Условимся впредь нули справа записывать, если только они являются значащими. Тогда, иначе говоря,

значащими являются все цифры числа а, кроме нулей слева.

В десятичной системе счисления всякое число а может быть представлено в виде конечной или бесконечной суммы (десятичной дроби):

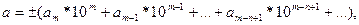
где , - первая значащая цифра, m - целое число, называемое старшим десятичным разрядом числа а.

Например, 518,3 = 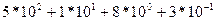, m=2.

Пользуясь записью 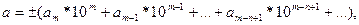, введем понятие о верных десятичных знаках (в значащих цифрах) приближенно-

го числа.

Определение. Говорят, что в приближенном числе а формы 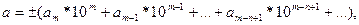n - первых значащих цифр ,

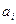где i= m, m-1,..., m-n+1 являются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n-й значащей цифрой:

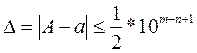
В противном случае последняя цифра 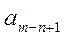называется сомнительной.

При записи приближенного числа без указания его погрешности требуют, чтобы все записанные цифры

были верными. Это требование соблюдено во всех математических таблицах.

Термин “n верных знаков” характеризует лишь степень точности приближенного числа и его не следует понимать так, что n первых значащих цифр приближенного числа а совпадает с соответствующими цифрами точного числа А. Например, у чисел А=10, а=9,997 все значащие цифры различны, но число а имеет 3 верных значащих цифры. Действительно, здесь m=0 и 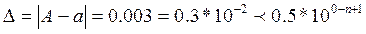n=3 (находим подбором).

На практике отыскание n из 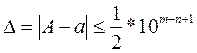при известных 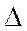и m требует решения нелинейного неравенства, что составляет непростую задачу. Правильный выбор n возможен из тривиального линейного равенства по следующей методике.

Величину 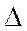записываем в виде 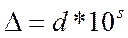, где 0,05<d≤0,5, что всегда возможно. Тогда в 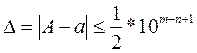неравенство для

коэффициентов выполняется (d≤1/2), основания степеней справа и слева одинаковы, поэтому можем приравнять показатели степеней: s=m-n+1, поэтому n=m-s+1.

ТЕОРЕМА 1. Если положительное приближенное число а имеет n верных десятичных знаков, то для относительной погрешности 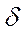этого числа справедлива оценка:

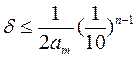
где 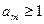- первая значащая цифра числа а.

Доказательство. Пусть число а определено формулой 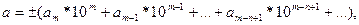со знаком + перед скобкой. По условию а имеет n верных знаков, следовательно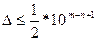

Тогда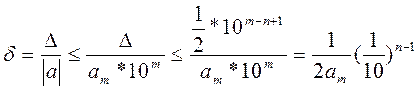

Следствие. В качестве предельной относительной погрешности числа а можно принять

Дата добавления: 2015-04-24