
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Достаточные условия сходимости метода простой итерации (теоремы, оценки погрешностей)
|
|
|
|
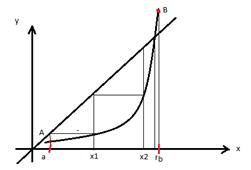
Метод простых итераций для численного решения алгебраических или трансцендентных уравнений. (Суть метода и геометрическая интерпретация).
Алгоритм
1. Задается начальное приближение 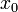 .
.
2. Пока не выполнено условие остановки, в качестве которого можно взять 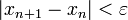 или
или 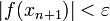 (то есть погрешность в нужных пределах), вычисляют новое приближение:
(то есть погрешность в нужных пределах), вычисляют новое приближение: 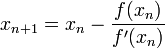 .
.
Суть метода:
f(х)=0 (1) непрерывная функция заменим эквивалентным уравнением 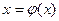 (2).
(2).
Выберем каким либо способом грубое приближение корня и обозначим его х0.
Подставим х0 в правую часть уравнения (2), получим х1= 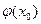 , х2=
, х2= 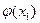 ….. хn=
….. хn= 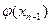 (3)
(3)
Если последовательность окажется сходящейся то 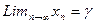
Переходя к пределу в равенстве (3), получим 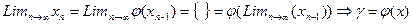 Стало быть
Стало быть  является корнем уравнения (2)
является корнем уравнения (2) 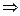 и уравнения (1).
и уравнения (1).
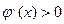
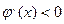
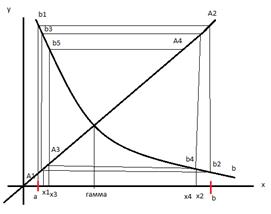
Теорема сходимости:
Пусть существует функция  определена и дифференцируема на отрезке [a,b]. Причем все значения функции
определена и дифференцируема на отрезке [a,b]. Причем все значения функции  принадлежат отрезку [a,b], тогда если существует правильная дробь 0<q<1 такая что
принадлежат отрезку [a,b], тогда если существует правильная дробь 0<q<1 такая что 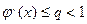 для
для 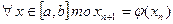 где n=0,1,2… сходятся независимо от начального приближения
где n=0,1,2… сходятся независимо от начального приближения 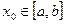 , причем предельное значение
, причем предельное значение 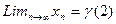 и этот корень единственный.
и этот корень единственный.
Доказательство:
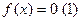 приводя к эквивалентному виду
приводя к эквивалентному виду
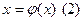
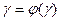
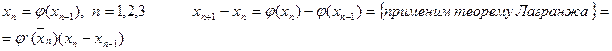
Обозначим за q=sup 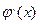
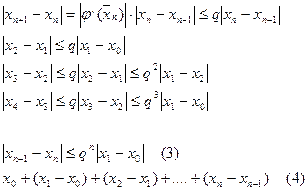
Последовательность приближений хn есть частичные суммы Sn+1 ряда 4
S2=x1
S3=x2……
Sn+1=xn
Члены ряда 4 по абсолютной величине начиная с 3, меньше членов арифметической прогрессии со значениями 0<q<1, q;q2;q3;…;qn.
Геометрическая прогрессия является сходящейся, значит существует 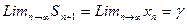
В силу непрерывности  можно записать
можно записать 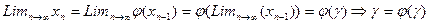 , значит этот корень уравнения (2).
, значит этот корень уравнения (2).
Докажем единственность:
Пусть существует 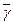 которая является корнем (2)
которая является корнем (2)
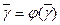 , найдем
, найдем 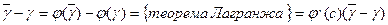
с- внутренняя точка отрезка [a,b].
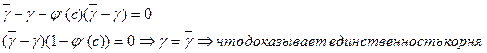

Замечание 1:
1. Константа q – носит название константы Липшиця.
|
|
|
2. Наша теорема справедлива, если функция  будет определена и дифференцируема на интервале (-
будет определена и дифференцируема на интервале (-  , +
, +  ), но лишь в том случае, когда константа Липшиця
), но лишь в том случае, когда константа Липшиця 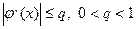 .
.
3. В условиях теоремы метод итерации сходится для любого х0 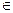 [a,b] благодаря чему он является самоисправляющийся, т.е. отдельные ошибки в вычислениях не влияют на результат.
[a,b] благодаря чему он является самоисправляющийся, т.е. отдельные ошибки в вычислениях не влияют на результат.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 986; Нарушение авторских прав?; Мы поможем в написании вашей работы!