Интерполяционный многочлен Лагранжа (вывод, доказательство единственности)

Первая интерполяционная формула Ньютона (общая формула и формулы для линейного и квадратичного интерполирования).

Пусть y=f(x) задана своими точками y_i=f(x_i) i=0,n, причем x_i=x₀+ih. h - шаг интерполирования.

Рассмотрим многочлен степени y=P_n(x) обладающий условием P_n(x_i)=y_i (1)

Условие (1) равносильно равенству:

Полагая в равенстве (3) x=x₀ получим, что P_n(x₀)=a₀ следовательно a₀=y₀.

Вычисляя 1-ю конечную разность полинома P_n(x) (см (2)) и полагая, что x=x₀ мы получаем, что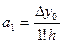

Находя вторую конечную разность и пологая что x=x₀ 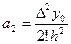, продолжая процесс мы получим, что i=0,n.

Подставляя в равенство (3) зная коэффициент a_i, получим:

- первый полином Ньютона.

Обычно первый полином Ньютона записывается в более удобном виде:

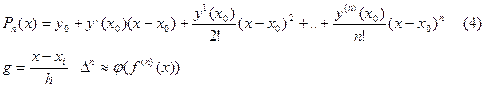
Формула (4) неудобная для практического применения. Поэтому был введен второй интерполяционный полином Ньютона:

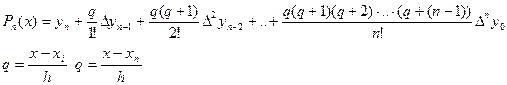
Стоит задача построить алгебраический многочлен ln(x) обл. двумя свойствами.

1. Степень многочлена 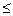h

2. Значение многочлена в ключевых точках h_n(x_i)=f(x_i)

Предложено построить вспомогательный полином p_i(x), i=0,n со свойствами

Первое равенство в формуле (1) позволяет на основании теоремы Безу записать

C_i- константа.

На основании (2) равенства в формуле (1)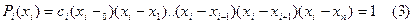

Выражая из формулы (3) c_i и подставляя в (2) окончательно получим

Тогда искомый полином Ln(x) запишется

Дата добавления: 2015-04-24