Метод Эйлера для систем дифференциальных уравнений

Выбрав достаточно малый шаг h построим систему равностоящих точек

Xi=x+ih (io=1,2,…) {xi=xi-1 + h}

Что бы решить задачу Коши 1 и 2 нужно найти интегрированную кривую, которая проходит через точку М0(х0,у0). В методе Эйлера искомую кривую заменяют ломанной MiMi+1 – прямолинейные отрезки расположены между прямыми x=xi; x=xi+1, причем эти отрезки имеют наклон, который равен

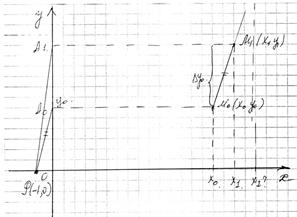
Угловой коэффициент через М0 проводим отрезок = , через М1 проводим отрезок = и параллельно проводим отрезок = 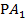отсюда следует М2(х2,у2) построим ломанную, которая проходит через начальную точку и yi+1= yi+ ; *f(xi,yi)=h*yi’

Метод Эйлера явл простейшим численным методом интегрирования дифференциального уравнения.

Недостатком этого метода является

1. Малая точность

2. Систематическое накопление ошибок

Можно доказать что если правая часть F(x,y) (1) непрерывна, то последовательность ломанных Эйлера при h->0 на достаточно малом отрезке например [x0,x0+h ] будет стремиться к искомой интегральной кривой у=у(х). Этот метод легко распространяется на систему ДУ.

Пример: пусть дана задача Коши

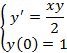
Отрезок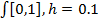

i-номер итеррации

х-аргумент

у-ф-ция

Аналог.Решение y=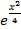

Метод Эйлера обладает малой точностью и дает удовлетворительный результат лишь при малых значениях h, это понятно, т.к по существу находя последующее значение интегральной ф-ции двумя членами ряда Тейлора на каждом частичном [xi,xi+1]

Yi+1=yi+hyi’ мы получаем погрешность порядка . Кроме того при вычислении на следующем отрезке исходные данные не явл точными, поэтому есть смысл рассмотреть модификацию метода Эйлера.

Дата добавления: 2015-04-24