Постановка задачи интерполирования

Обобщенная степень

Постановка задач аппроксимации функции, общей задачи интерполирования, простейшей задачи интерполирования.

Обобщенной n степенью числа х называется произведение n сомножителей первой из которых является х, а каждый следующий сомножитель, на h меньше предыдущего.

Х^[n]- обозначение.

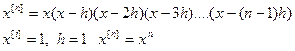
Найдем конечную разность для обобщенной степени.

f(x)=x^[n], тогда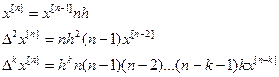

Простейшие задачи интерполирования заключаются в следующем:

Пусть на отрезке [a,b] задана n+1 точка x₀,x₁,x₂….x_n.

Эти точки называются узлами интерполирования, для этих узлов интерполирования известно значение некоторых функций y=f(x)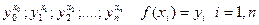

Требуется построить функцию y=F(x) такую что F(x₀)=y₀, F(x₁)=y₁, F(x₂)=y₂….F(x_n)=y_n

Функция F(x) называется интерполирующей.

Аналитическое выражение f(x) очень сложное или неизвестное.

Геометрически это означает, что надо найти y=F(x) с некоторыми дополнительными свойствами в частности F(x) проходит через точку (x_i,y_i), y_i=f(x_i) i=1,n

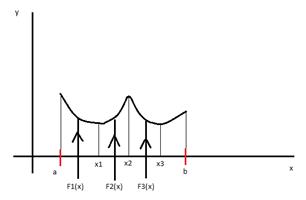
Задача в такой постановке может иметь бесконечное множество решений.

Задача становится однозначно решаемой, если в качестве функции y=f(x) рассматривать полином y=P_n(x) степени не выше n, которая удовлетворяет условию P_n(x_i)=y_i i=0,n.

n- количество точек. Полученная интерполирующая функция часто используется для приближенного вычисления значений функции y=f(x) в точках не совпадающих с узлами интерполяции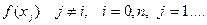

Такая операция называется интерполированием функции f(x).

Различают интерполирование в узком смысле 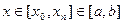и в широком 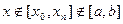. Данная операция носит название экстраполированием.

Дата добавления: 2015-04-24