Метод Эйлера для решения скалярной задачи Коши (вывод расчетной формулы, геометрический смысл) и его недостатки

Задача Коши состоит в том, что бы найти решение 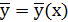, которое бы удовлетворяла системе (5) или соответствующему векторному уравнению(6) или условию 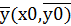(7)

Х0- фиксированное значение,

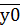-значение yi в х0

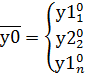
Геометрически это значит, что требуется отыскать интегральную кривую 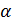. Которая проходит через заданную точку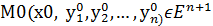

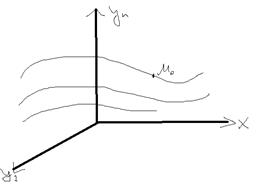
Для системы ОДУ можно сформулировать теорему о существовании и единственности решения.

Теорема: Пусть в некоторой окрестности начального значения

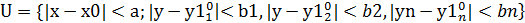
Система (5)обладает след.свойствами

1.Правые части (5)определены и непрерывны в облаcти U

2. Ф-циия fi в окресности U должны удовлетворять условию Липнинца (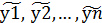); (y1,y2,…,yn)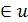

|f(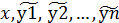)-fi(x,y1,y2,…,yn)<N 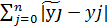(8)

Условие (8) гарантирует существование единственного решения, которое определено в окрестности точки |x-x0|<h,h>0

При выполнении условия (1),(2),(3)

Y’=f(x,y);

y=y(x) (2)

y0=y(x0) (3)

Задача Коши разрешима и имеет единственное решение, т.е через точку М0 проходит единственная интегральная кривая.

Замечание: вместо условия Липшица достаточно потребовать ограничения производных 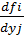, I,j-=1,n. Тогда за N можно взять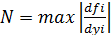

Однако для линейных ф-ций f(x,y) как правило общее решение ОДУ не удается найти, поэтому возникают потребности в создании большого числа приближенных методов решения дифференциальных уравнений. Все эти методы можно разделить на 3 группы:

1.Аналитические методы, которые дают приближенные решения в виде аналитических выражений.

2. Графические методы, которые дают приближенное решение в виде графика

3. Численные методы, которые достигаются приближенным решением в виде таблиц.

Среди численных методов можно выделить и рассмотреть:

1. Интегрированные ДУ с помощью степенных рядов.

2. Метод последовательных приближений.

3. Метод Эйлера

Дата добавления: 2015-04-24