Постановка задачи численного решения обыкновенных дифференциальных уравнений

Формула Симпсона и ее остаточный член (вывод основной и обобщенной формул, запись остаточного члена, оценка шага интегрирования)

Формула трапеции и ее остаточный член(вывод основной и общей формулы, запись остаточного члена, оценка шага интегрирования)

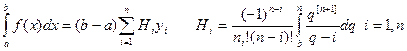
1. n=1

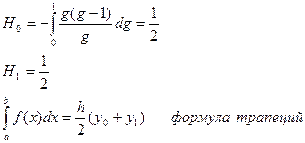
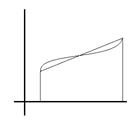
Оценка:

Интегрируя выражение по h и воспользовавшись теоремой о среднем получим

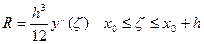
Формула получается при n=2 из формулы Ньютона – Котеса

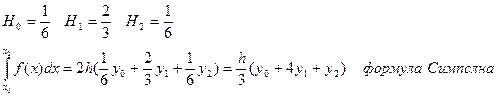
Оценка: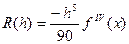

Разбивая промежуток 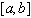на 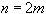равных частей точками 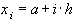, 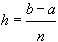и применяя формулу 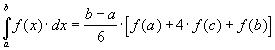(71)

(71)

к каждому из частичных промежутков 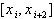длины 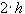, 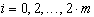получаем обобщенную формулу Симпсона:

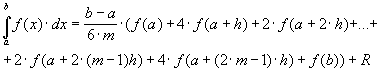
Оценка погрешности этой формулы следует из 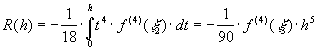(72)

следует

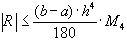(74)

П ОДУ 1-ого порядка наз-ся уравнение вида y’=f(x) (1)

Рассмотрим основную задачу для ОДУ Задача Коши.

Она состоит в том что бы найти решение в ур 1 удовлетворяющее начальному условию y=f(x) (2)

У0=у(х0) (3)можно найти ед. интегрированную кривую которая бы удовлетворяла условию (3). Если правая часть ур (1) непрерывна в некоторой области R={|x-x0|<a;|y-y0|<b}, то существует одно решение, это решение единственно, если в области R выполняется условие применяется для любого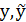

|f(x,y)-f(x, 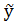)|≤N| 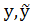| - условие

N-константа зависит от области R.

Если ф-ция 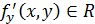имеет ограниченную производную по y,то логично N=max| 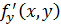|, для любого х,у

Для дисперсного ур n-ого порядка 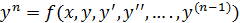задача коши будет иметь вид

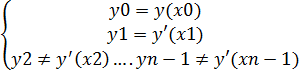(4)

В приложениях часто встречаются ОДУ. Если ограничиться только рассмотрением только нормальной системы n-ого порядка

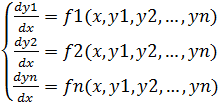(5)

x-независимая переменная

у1- исходная ф-ция

Если система диф.ур содержит производные высших порядков и разряжена относительно старших производных, то путем введения новых переменных ф-ции мы систему (**) можем свести к виду (5)

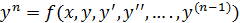
Обозначения: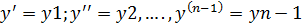

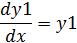
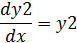
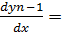f(x,y1,y2,…,yn-1)

При решении системы ОДУ можно воспользоваться векторным обозначением ф-ции

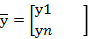
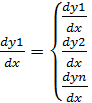
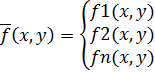
Тогда система 5 в векторном виде 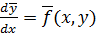(6)

Дата добавления: 2015-04-24