Понятие устойчивости решения дифференциального уравнения. Асимптотическая устойчивость. Теорема Ляпунова об устойчивости

Теорема Ляпунова: Если для системы дифференциальных уравнений i=1…n существует знакоопределенная функция V(x1,x2..xn), полная производная которой составлена в соответствии с системой, есть функция знакопостоянная знака противоположного знаку функции V, то решение этой системы устойчиво. (если знакопостоянную заменить на знакопеременную, то решение асимптотически устойчиво)

Рассмотрим дифференциальное уравнение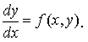

Пусть некоторое фиксированное решение y = φ(x) этого уравнения существует при всех x ≥ x ₀.

Решение y = φ(x) уравнения называется устойчивым по Ляпунову при x ≥ x ₀, если для любого ε > 0 существует число δ > 0(зависящее, вообще говоря, от ε) такое, что:

1) решение y = y (x) задачи Коши с начальным условием y (x ₀), | y (x ₀) − φ(x ₀) | < δ, существует при всех x ≥ x ₀;

2) для всех таких решений справедливо неравенство | y (x) − φ(x) | < ε, при всех x > x ₀. Геометрически это означает, что интегральные кривые y = y (x), близкие в момент x = x ₀ к интегральной кривой y = φ(x), остаются близкими к ней и на всем промежутке [x₀, ∞).

Решение y = φ(x) называется неустойчивым по Ляпунову при x ≥ x ₀, если существует число ε > 0 такое, что для любого δ > 0

найдутся решения y = y _δ(x) и значение x ₁ = x ₁(δ) > x ₀ такие, что хотя | y _δ(x ₀) − φ(x ₀) | < δ, но | y (x ₁) − φ(x ₁) | ≥ ε.

Рассмотрим дифференциальное уравнение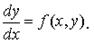

Пусть некоторое фиксированное решение y = φ(x) этого уравнения существует при всех x ≥ x ₀.

Решение y = φ(x) уравнения называется асимптотически устойчивым по Ляпунову при x → ∞, если

1)это решение устойчиво по Ляпунову при x ≥ x ₀;

2)для любого δ > 0 и для всех решений y = y (x) задачи Коши с начальным условием y (x ₀), | y (x ₀) − φ(x ₀) | < δ, разность | y (x) − φ(x) | → 0 при x → ∞.

Геометрически это означает, что интегральные кривые y = y (x), близкие в момент x = x ₀ к интегральной кривой y = φ(x), становятся как угодно близкими к ней при x → ∞.

Дата добавления: 2015-04-24