ІІ Середня арифметична зважена

І Середня арифметична проста

Суть середніх величин та їх значення в статистиці. Види середніх величин, порядок їх обчислення та умови застосування.

В залежності від способу розрахунку середньої величини розрізняють декілька видів середніх величин:

1. середня арифметична проста;

2. середня арифметична зважена;

3. середня гармонічна;

4. середня квадратична;

5. середня геометрична;

6. середня хронологічна

7. мода і медіана.

Для розрахунку середніх величин приміняють наступні умовні позначення:

X –окреме значення досліджуваної ознаки X –середнє значеннядосліджуваної ознаки n –число одиницьдосліджуваної ознаки f -частота повторень того самого значення ознаки W- загальна кількість дослід жувального явища (W = x * f)  

Застосовується у тих випадках, коли відомі значення ознаки кожної одиниці сукупності.

Вона утворюється шляхом простого підсумовування усіх варіант показника і розподілом отриманої суми на загальне число усіх варіант.

X=

x1+ x2 +x3+…+x n n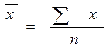

;

У деяких випадках статистична сукупність може бути згрупована і представлена у вигляді варіаційного ряду розподілу.

Застосовується у тих випадках, коли вихідні дані наведені у вигляді варіаційного ряду розподілу, у якому частоти окремих значень ознаки нерівні. Для розрахунку середнього значення ознаки варіанта помножується на число повторень тобто на частоту і ділиться на загальну кількість усіх варіант.

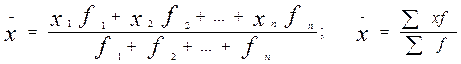
Якщо середня арифметична зваженазастосовується в тих випадках, коли варіанти виражені у вигляді інтервалів у цьому випадку за варіанту приймають середнє значення інтервалу.

Для визначення середньої величини в інтервальному ряді розподілу спочатку треба визначити центр інтервалу в кожній групі.

Центр інтервалу =

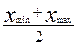
Якщо в рядах розподілу є відкриті інтервали, то в таких рядах величина інтервалу першої групи умовно дорівнює величині інтервалу наступної групи, а величина інтервалу останньої групи – величині інтервалу попередньої групи.

Дата добавления: 2015-04-24