Ряди розподілу, їх види та правила побудови. Засоби графічного зображення розподілу одиниць сукупності

VІ Середня хронологічна

ІІІ Середня гармонічна

Застосовується у тих випадках, коли є данні про значення ознаки та обсяг ознаки, частоти не задані, а входять як співмножники в показники обсягу ознак (коли неможна примінити для розрахунку середню арифметичну зважену, тобто не визначені частоти).

Середня гармонічна проста: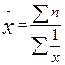

Середня гармонічна зважена: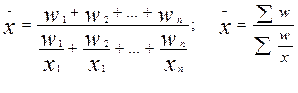

Обчислюється для визначення середнього значення моментального ряду динаміки, тобто коли є дані на визначений момент часу, тобто на конкретну дату.

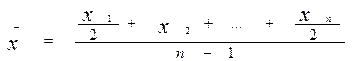
Після обробки кількісних значень, їх систематизації, ми дістаємо певний цифровий ряд, який називається статистичний ряд. Він має дві форми: ряд розподілу і динамічний ряд.

Ряд розподілу – це впорядкований розподіл сукупності на групи за певною варіюючою ознакою, розташованою в певному порядку (зростання, спадання тощо).

Виділяють атрибутивні і варіаційні ряди розподілу.

Ряд розподілу одиниць сукупності, в основу якого покладено якісні ознаки називається атрибутивним. Прикладом атрибутивного ряду розподілу може бути розподіл населення на міське і сільське. Ряд розподілу одиниць сукупності за ознакою, що має кількісне вираження, називається варіаційним. Варіаційний ряд розподілу має свої особливості. Він складається з двох елементів: варіантів і частот.

Варіантами називають числові значення розмірів кількісної ознаки. Числа, які відповідають цим варіантам, називаються частотами. Частоти можуть виражатися як в абсолютних, так і у відносних одиницях (напр. відсотках).

Відповідно до варіації ознаки, варіаційні ряди розподілу можуть бути дискретними і інтервальними. В дискретному ряді розподілу кількісна ознака приймає тільки цілі значення. Коли значення варіантів ряду виражено у вигляді інтервалу, такий ряд розподілу називається інтервальним.

Накопичення часток по мірі зростання (спадання) ознаки називається акумулятивна частка.

За характером розподілу варіаційні ряди можуть бути симетричні і асиметричні.

Ряд розподілу, де частоти спочатку наростають, а потім спадають, називається симетричним. Ряд розподілу, в якому частоти розташовані несиметрично від середини, називається асиметричним або скошеним.

Основними способами графічного зображення рядів розподілу є огіва, гістограма, полігон, кумулята і крива Лоренца.

Огіва – графічне зображення ранжированого ряду розподілу. На осі абсцис відкладають номер одиниці сукупності у ранжированому ряду, а на осі ординат – значення досліджуваної ознаки (варіанти).

Гістограма (стовпчикова діаграма розподілу) застосовується для зображення інтервальних варіаційних рядів. При її побудові на осі абсцис відкладають відрізки, які зображують інтервал. Площа кожного стовпчика повинна бути пропорційною частотам (частостям). Для рівних інтервалів ширину стовпчиків беруть однаковою, а висота має бути пропорційною частотам. При нерівних інтервалах ширина стовпчиків має бути пропорційною величині інтервалу у кожній групі, а висоту стовпчиків зменшують у стільки разів, у скільки збільшується величина інтервалу.

Полігон розподілу застосовують для зображення дискретних та інтервальних варіаційних рядів. Координатами точок при цьому є варіанти (з інтервальними рядами середини інтервалів) і частоти, що відповідають цим варіантом. Точки з’єднують прямими лініями. Щоб замкнути полігон, крайні точки з’єднують із серединами інтервалів, у яких частоти дорівнюють нулю.

Кумулята – графічне зображення варіаційного ряду з нагромадженими частотами (частостями). Для її побудови на осі абсцис відкладають варіанти, а на осі орданит – нагромаджені частоти (частості) які показують, скільки одиниць сукупності мають значення ознаки, що не перебільшує цього значення. Кумуляту застосовують при порівнянні різних варіаційних рядів. На використанні кумуляти грунтується критерій лямбда, який визначає вірогідність різниць двох розподілів.

Крива Лоренца – це спосіб графічного зображення рівня концентрації явища. Для її побудови на осі координат наносять процентну масштабну шкалу від 0 до 100. На осі абсцис відкладають нагромаджені частості, а на осі ординат – нагромаджені відносні обсяги варіюючої ознаки, вираженої в процентах. Загальний обсяг явища одержують, підсумовуючи добутки від множення варіантів на їх частості. При рівномірному розподілі ознаки певному проценту одиниць сукупності відповідає такий самий процент значень сумарної ознаки. На графіку лінією рівномірного розподілу є діагональ квадрата. При нерівномірному розподілі лінія концентрації становить увігнуту криву залежно від рівня концентрації ознаки. Її відхилення від діагоналі квадрата характеризує ступінь концентрації явища. Чим більша нерівномірність у розподілі частот, тим більше відхилення лінії концентрації від діагоналі.

Кожний ряд розподілу можна зобразити за допомогою відповідної кривої, яку називають кривою розподілу.

До одновершинних належать такі криві, графіки розподілів яких мають один максимум частот. Їх поділяють на симетричні (в яких максимум частот припадає на середину ряду) і асиметричні (в яких максимум частот припадає на початок або кінець ряду). Якщо частоти нарастають швидче ніж спадають, асиметрія буде правосторонньою, а якщо навпаки – лівосторонньою.

До багатовершинних належать такі криві, графіки розподілів яких мають кілька максимумів частот. Багатовершинність розподілу свідчить про неоднорідність сукупності.

Характеристиками розподілу є середня величина, мода, медіана, квартилі і доцилі.

Дата добавления: 2015-04-24