Види дисперсії. Властивості загальної дисперсії

Дисперсія ознаки, або середній квадрат відхилень σ²_х дорівнює різниці між середнім квадратом значень ознаки %² і квадратом середнього значення ознаки 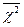. Таким чином, не обчислюючи відхилень можна обчислити дисперсію. Загальна дисперсія, яку вже було розглянуто, характеризує загальну варіацію ознаки під впливом усіх умов і причин, що зумовили цю варіацію.

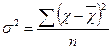
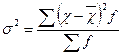
Для визначення впливу постійного фактора на розмір варіації потрібно розбити всю сукупність на групи та знайти, як змінюється результат під дією чинника, покладеного в основу групування. Для цього попередньо необхідно обчислити для кожної групи середню величину ознаки, групові (часткові) дисперсії, середню з групових та міжгрупову дисперсію.

Групова дисперсія дорівнює середньому квадрату відхилень окремих значень ознаки всередині групи від середньої арифметичної відповідної групи. її можна обчислити як середню просту і як зважену за формулами:

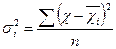
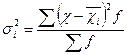
або спрощеним способом: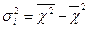

Ця дисперсія відображує варіацію ознаки лише за рахунок умов і причин, що діють всередині групи.

Середня з групових дисперсій — це середня арифметична зважена з групових дисперсій:

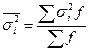
Міжгрупова дисперсія дорівнює середньому квадрату відхилень групових середніх 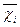від загальної середньої :

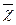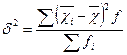
де σ²_— міжгрупова дисперсія; χ_і — середня кожної окремої групи; 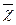— загальна середня всієї сукупності; f_і — частоти.

Міжгрупова дисперсія характеризує варіацію результативної ознаки за рахунок групувальної ознаки.

Між наведеними видами дисперсій існує певне співвідношення: загальна дисперсія дорівнює сумі середньої з групових дисперсій та міжгрупової дисперсії.

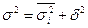
Це співвідношення називають правилом додавання дисперсій, за яким, знаючи два види дисперсій, можна визначити третій.

Дата добавления: 2015-04-24