Диференціальні закони збереження енергії. Тензор напружень

Аксіоми суцільного середовища

(1) Аксіома простору–часу. Суцільне середовище є підмножиною евклідового простору R³, WÎR³. Час – абсолютний (незалежний від подій).Дана аксіома обмежує моделі МСС рамками Ньютонівської механіки. (Евклідів простір – векторний простір зі скалярним добутком)

(2) Аксіома матеріального континууму (суцільності). Суцільне середовище у кожний момент часу є матеріальним континуумом.На множині W визначені адитивні невід'ємні неперервні диференційовні (за винятком, можливо, окремих точок та поверхонь) функції: маса М та внутрішня енергія Е. (Континуум – незліченна множина або множина, рівнопотужна множині дійсних чисел в інтервалі (0,1))

(3) Аксіома руху середовища. Існує взаємооднозначне відображення (гомеоморфізм) xÎW₀ → g_t (x,t)ÎW_t, (t Î R) між всіма точками середовища в моменти часу t₀ та t. Відображення t→g_t є ізоморфним (взаємнооднозначим) та для кожної траєкторії з початком в xÎW₀, t→g_t(x) є неперервним і кусково–неперевно диференційовним.

(4) Аксіома сил і потоку тепла. Зовнішня масова сила діє не просто на тіло в цілому, а розподіляється між усіма його точками.

Узагальнення ньютонівського поняття сили полягає в тому, що окрім реакції на зовнішні масові сили, слід враховувати ще й внутрішню взаємодію сусідніх матерільних точок, яка відбувається по поверхні їх контакту.

(5) Аксіоми балансу – збереження маси, імпульсу, моменту імпульсу, енергії. Ці аксіоми складають інтегральну модель суцільного середовища. Параметри моделі – густина, швидкість, питома внутрішня енергія, густина масових сил, напруження внутрішніх сил, густина потку тепла.

Інтегральна модель є доволі складною для дослідження, що у значній мірі викликано демократичністю вимог до гладкості її функцій.

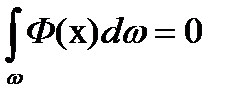У багатьох же практичних застосуваннях наперед відома гладкість шуканих розв'язків дає змогу переформулювати інтегральну модель у систему диференціальних рівнянь у часткових похідних, котра більш явно надається для дослідження математичними засобами.

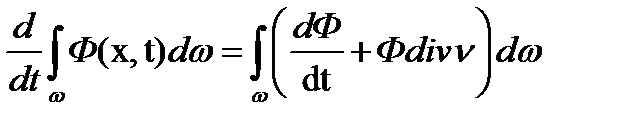Твердження 1. Якщо неперервна в області D⊂RⁿфункціяФ: D→R^k така, що для довільного об'єму ω⊂D, то Ф(х) = 0 в D.

Твердження 2.

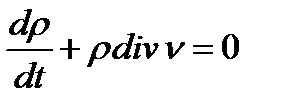
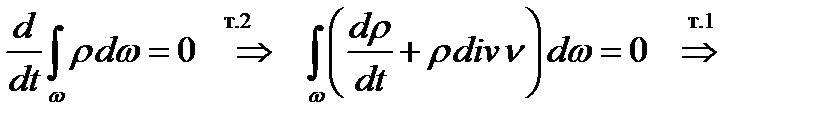Аксіома збереження маси:

Рівняння нерозривності.

Отримана диференціальна модель, незважаючи на істотні обмеження щодо очікуваної гладкості розв'язків, все ще описує широкий клас задач різноманітних суцільних середовищ (газів, рідин та твердих тіл), через що залишається надто складною для прямих практичних застосувань.

Тензор напружень – це тензор другого рангу, яким описуються сили, що виникають в твердому тілі при деформації.

Тензор рангу (m, n) над векторним простом V – це елемент тензорного добутку mпросторів Vта nспряжених просторів V*:

Тензорний добуток просторів – те ж, що і звичайний матричний добуток.

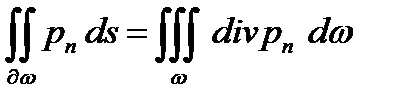Тензор напружень використовують для отримання диференціальних аналогів аксіом інтегральної моделі. Тут потрібно перейти від поверхневих інтегралів до об'ємних. Даний перехід забезпечує формула Остроградського–Гауса:

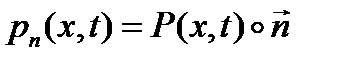У кожній точці об'єму потрібно визначити набір величин, який здатен презентувати зусилля на будь–яку площу з нормаллю n, через точку якої проходить зусилля. В МСС роль такого набору величин грає тензор напружень Р

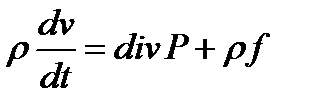Запишемо тепер закон зберження іспульсу у новому вигляді:

Отримана диференціальна модель, незважаючи на істотні обмеження щодо очікуваної гладкості розв'язків, все ще описує широкий клас задач різноманітних суцільних середовищ (газів, рідин та твердих тіл), через що залишається надто складною для прямих практичних застосувань.

Дата добавления: 2015-05-08