Вимоги до даних

Лабораторна робота № 15

Оцінка статистичної значимості експериментальних результатів

План.

1. Актуалізація знань студентів.

(нуль-гіпотеза, t-критерій, можливі похибки при відторгненні або невідторгненні нуль-гіпотези)

t-критерій Стьюдента – загальна назва для класу методів статистичної перевірки гіпотез (статистичних критеріїв), заснованих на порівнянні з розподіленням Стьюдента. Найбільш часті випадки застосування t-критерію пов'язані з перевіркою рівності середніх значень в двох вибірках.

Історія. Даний критерій був розроблений Уїльямом Госсеттом для оцінки якості пива в компанії Гінес. У зв'язку із зобов'язаннями перед компанією з нерозголошування комерційної таємниці (керівництво Гінесу вважало таким використання статистичного апарату в своїй роботі), стаття Госсета вийшла в 1908 році в журналі «Біометрика» під псевдонімом «Student» (Студент).

Для застосування даного критерію необхідно, щоб початкові дані мали нормальне розподілення. У разі застосування двох вибіркового критерію для незалежних вибірок також необхідне дотримання умови рівності дисперсій. Існують, проте, альтернативи критерію Стьюдента для ситуації з нерівними дисперсіями.

Двохвибірковий t-критерій для незалежних вибірок

У випадку з розміром вибірки, що трохи відрізняється, застосовується спрощена формула наближених розрахунків:

; .

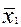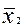Де і – середні арифметичні для результатів отриманих при першому і другому значеннях незалежної змінно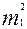ї.

і 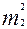– це середні похибки вимірювання.

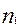і – кількість результатів експериментальних, отриманих при 2 і 1 відповідно значеннях незалежної змінної.

Порівнюємо отримані в експерименті значення t з табличним значенням з урахуванням ступенів свободи, рівних за формулою числу досліджуваних мінус два.

Якщо > критичне, то робиться висновок про те, що отримані результати є статистично значимими (не випадковими) лише такі результати підтверджують експериментальну або альтернативну гіпотези.

Якщо 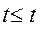критичне, то робиться висновок про статистичну не значимість експериментальних результатів. Такі результати не можуть підтвердити експериментальну або альтернативну гіпотези, вони вважаються отриманими випадково.

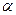критичне шукаємо у відповідній статистичній таблиці в залежності від числа і відповідного – рівня

Табличне значення t критичне дорівнює 2,1 при допущенні можливості ризику зробити помилкову думку в п'яти випадках із ста (рівень значимості = 5 % або 0,05).

Якщо отримане в експерименті емпіричне значення t перевищує табличне, тобто підстави прийняти альтернативну гіпотезу (H₁) про те, що учні експериментальної групи показують в середньому вищий рівень знань. У експерименті t=3,981, табличне t=2,10, 3,981>2,10, звідки слідує висновок про перевагу експериментального навчання.

Дата добавления: 2015-05-22