Взаимная корреляционная функция

Свойства автокорреляционных функций

Автокорреляционные функции играют большую роль в представлении случайных процессов и при анализе систем, оперирующих со случайными входными сигналами. Поэтому приведем некоторые свойства автокорреляционных функций стационарных процессов.

1. R_x(0) = M(X²(t)) = D_x(t).

2. R_x(t) = R_x(-t). Автокорреляционная функция является четной функцией. Это свойство симметрии графика функции исключительно полезно при вычислении автокорреляционной функции, так оно означает, что вычисления можно производить только для положительных t, а для отрицательных t можно их определить, используя свойство симметрии.

3.½R_x(t)½£ R_x(0). Наибольшее значение автокорреляционной функции, как правило, принимает при t = 0.

Пример. В случайном процессе X(t) = A Coswt, где А – случайная величина с характеристиками: М(А) = 0, D(A) = s², найти М(Х), D(Х) и R_x(t₁,t₂).

Решение. Найдем математическое ожидание и дисперсию случайного процесса:

М(Х) = М(A Coswt) = Coswt × М(А) = 0,

D(Х) = М((A Coswt-0)²) = М(А²) Cos²wt = s² Cos²wt.

Теперь найдем автокорреляционную функцию

R_x(t₁,t₂) = М(А Coswt₁× А Coswt₂) =

= М(А²) Coswt₁× Coswt₂ = s² Coswt₁× Coswt₂^.

Входной Х(t) и выходной Y(t) случайные сигналы системы можно рассматривать как двумерный векторный случайный процесс 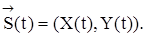Введем числовые характеристики этого процесса.

Математическое ожидание и дисперсия векторного случайного процесса 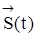определяется как математическое ожидание и дисперсия его компонент:

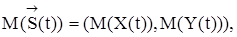
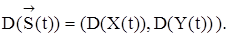
Корреляционную функцию 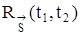векторного процесса 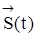введем с помощью матрицы второго порядка:

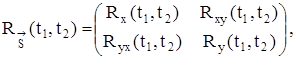
где R_xy (t₁, t₂) взаимная корреляционная функция случайных процессов X(t) иY(t), определяемая следующим образом

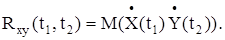
Из определения взаимной корреляционной функции вытекает, что

R_xy (t₁,t₂) = R_yx (t₂,t₁).

Нормированной взаимной корреляционной функцией двух случайных процессов X(t), Y(t) называется функция

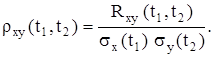
Определение. Если взаимная корреляционная функция случайных процессов X(t) и Y(t) равна нулю:

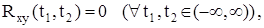
то случайные процессы называются некоррелироваными.

Для суммы случайных процессов X(t) и Y(t) автокорреляционная функция равна

R_x+y(t₁,t₂) = R_x(t₁,t₂) + R_xy(t₁,t₂) + R_yx(t₁,t₂) + R_y(t₁,t₂).

Для некоррелированных случайных процессов X(t) и Y(t) автокорреляционная функция суммы случайных процессов равна сумме автокорреляционных функций

R_x+y(t₁,t₂) = R_x(t₁,t₂) + R_y(t₁,t₂),

а значит и дисперсия суммы случайных процессов равна сумме дисперсий:

D_x+y(t) = D_x(t) + D_y(t).

Если 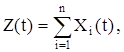где X₁(t),..., X_n(t) – некоррелированные случайные процессы, то 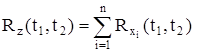и

При выполнении различных преобразований со случайными процессами часто удобно записывать их в комплексном виде.

Комплексным случайным процессом называется случайный процесс вида

Z(t) = X(t) + i Y(t),

где X(t), Y(t) - действительные случайные процессы.

Математическое ожидание, корреляционная функция и дисперсия комплексного случайного процесса определяются следующим образом:

M(Z) = M(X) + i M(Y),

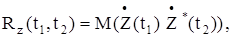
где знак * обозначает комплексное сопряжение;

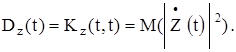
Пример. Пусть случайный процесс 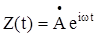, где w - постоянная величина, 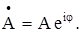Здесь А и j - независимые случайные величины, причем М(А) = m_A, D(A) = s², а j - равномерно распределенная случайная величина на интервале [0, 2p]. Определить математическое ожидание, корреляционную функцию и дисперсию комплексного случайного процесса Z(t).

Решение. Найдем математическое ожидание:

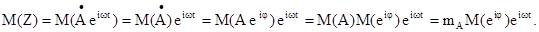
Используя равномерное распределение случайной величины j на интервале [0, 2p], имеем

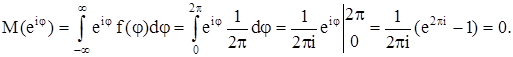
Автокорреляционная функция случайного процесса Z(t) равна

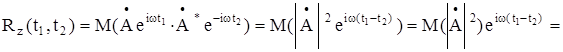
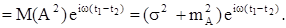
Отсюда имеем

D_z(t₁) = R_z(t_1, t₁) = s ² + m_A².

Из полученных результатов следует, что случайный процесс Z(t) стационарный в широком смысле.

Дата добавления: 2015-05-08