Линейное преобразование случайного процесса

При решении многих практических задач радиотехники приходится определять характеристики случайного процесса на выходе линейной системы. Линейная система осуществляет линейные операции над входным случайным процессом. Это значит, что если на вход системы поступает случайный процесс X(t), то на выходе этот процесс преобразуется в случайный процесс

Y(t) = A [X(t)],

где А – оператор (преобразование), обладающий свойствами:

A [a₁X₁(t) + a₂X₂(t)] = a₁ A [X₁(t)] + a₂[X₂(t)].

Здесь 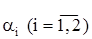постоянные величины.

Примеры линейных операторов

1. Оператор умножения на неслучайную функцию f(t):

Y(t) = A [X(t)] = f(t) X(t).

Определим математическое ожидание и автокорреляционную функцию случайного процесса Y(t):

m_y(t) = M(Y(t)) = M(f(t) X(t)) = f(t) M(X(t)),

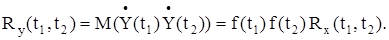
2. Оператор дифференцирования:

Представив производную в виде предела

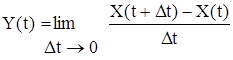
и применив операцию математического ожидания к правой и левой части равенства, получаем

Так как

То

3. Оператор интегрирования:

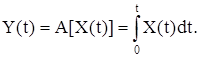
Представим интеграл в виде интегральной суммы

max Dt_i®0

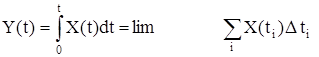
и применим к этому равенству операцию математического ожидания. Тогда имеем

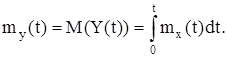
Автокорреляционная функция случайного процесса легко определяется:

Дата добавления: 2015-05-08