Заметим, что

(2)

Усредним теперь во времени левую часть равенства (1) с целью получения средней мощности случайного процесса

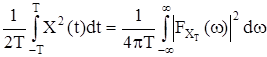(3)

Левая часть полученного равенства представляет собой квадрат эффективного значения функции X_T(t). Кроме того, для эргодического процесса при Т®¥ эта величина приближается к значению среднего квадрата случайного процесса M(X²(t)).

T®¥

В соотношении (3) нельзя перейти к пределу при Т®¥, так как не существует .

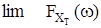Поэтому сначала возьмем математическое ожидание левой и правой частей этого равенства

и перепишем его, устремив Т® ¥. Тогда

Т®¥

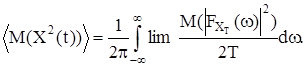
Для стационарного процесса

Поэтому получаем соотношение

Т® ¥

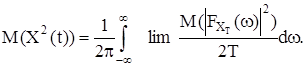(4)

Величина

Т® ¥  

называется спектральной плотностью случайного процесса. Укажем, что после выполнения операции усреднения по множеству реализаций (по ансамблю) справедлив переход к пределу при Т® ¥. Если X(t) - напряжение, то ([X] = B), S_x(w) имеет размерность а интеграл от S_x(w) в соответствии с (4) определяет средний квадрат этого напряжения, то есть

Более наглядная физическая интерпретация спектральной плотности может быть дана путем анализа средней мощности. Если X(t) – флуктуационное напряжение или ток, протекающий через резистор сопротивления 1 Ом, то М(Х²) есть средняя мощность, рассеиваемая этим резистором.

Спектральную плотность можно интерпретировать как среднюю мощность, сосредоточенную в пределах полосы частот шириной 1 Гц.

Вследствие этого спектральную плотность часто называют спектром плотности мощности.

От двусторонней спектральной плотности случайного процесса можно перейти к односторонней, где фигурирует обычно частота f. С этой целью запишем

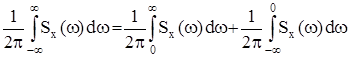
и в первом интеграле сделаем замену переменной, положив w = 2pf, а во втором - w = - 2pf.

Тогда

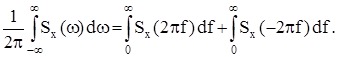
Так как в силу соотношения (2) функция S_x(w) = S_x(-w), то есть является четной функцией, то

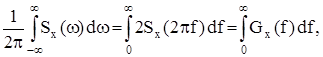
где

и

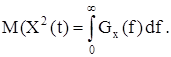
Представим интеграл в этом соотношении в виде интегральной суммы

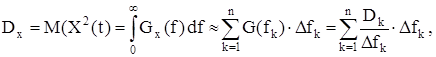
где D_k – дисперсия случайного процесса на k-ой гармонике. Отсюда получаем, что G_x(f) = D_k/Df_k – дисперсия (мощность) k-ой гармоники, отнесенная к полосе частот Df_k, то есть спектральная плотность дисперсии (мощности) случайного процеса.

Пример. Стационарный случайный процесс имеет двухстороннюю спектральную плотность

Определить среднюю мощность процесса, рассеиваемую на резисторе сопротивлением 1 Ом в диапазоне изменения w от –4 до 4.

Решение Средняя мощность процесса M(X²(t)) для указанного диапазона w равна:

автокорреляционная функция случайный процесс

В радиотехнике часто используется понятие "белого шума". Под "белым шумом" принято понимать стационарный случайный процесс, спектральная плотность которого постоянна на всех частотах. Термин "белый шум" образно подчеркивает аналогию со светом, у которого в пределах видимого диапазона частот интенсивность всех спектральных составляющих примерно одинакова. Белый шум является математической моделью процесса, который реально в природе не существует, так как мощность его равна бесконечности. Однако это удобная модель для описания широкополосных случайных процессов систем, в полосе пропускания которых спектр можно считать постоянным.

Размещено на Allbest

Дата добавления: 2015-05-08