Означення невизначеного інтеграла. Основні властивості. Методи інтегрування

НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ

Ред.]Рух проти колективізації і радянська протидія

В період колективізації в Україні відбулися 7382 бунти селян і акти масової непокори, 15 з яких визнані як широкомасштабні озброєні повстання проти Радянської влади. У 20-30х роках була справжня селянська війна. Окрім масових виступів селяни вели боротьбу поодинці й дрібними групами — влаштовуючи терор більшовикам. Висилку селян здійснювали в округи Північного краю — 70 тис. сімейств, Сибіру — 50 тис. сімейств, Уралу — 20-25 тис. сімейств, Казахстану — 20-25 тис. Районами висилки були необжиті і малообжиті місцевості, де висланих використовували на сільськогосподарських роботах або промислах (ліс, риба тощо). Реальну кількість висланих важко підрахувати. Потрібно враховувати, що сім'ї могли бути до 12 осіб^[1]. В зв'язку з необжитістю деяких місцевостей, висилка була фактично смертним вироком.

Функцію F(x) називають первісною для функції f(x) на проміжку Х, якщо в кожній точці виконується умова .

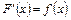Множину всіх первісних для функції f(x) на проміжку Х називають невизначеним інтегралом від функції f(x) і позначають так:

, (6.1)

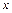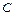де – підінтегральна функція; – підінтегральний вираз; – змінна інтегрування; – одна з первісних; – довільне дійсне число; 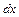– диференціал аргументу функції. Він визначає змінну по якій ведеться інтегрування.

Наприклад:

, , .

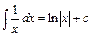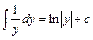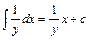Тому наявність диференціала під інтегралом є необхідним. Такий вираз немає змісту. Не відомо по якій змінній ведеться інтегрування.

Операцію знаходження невизначеного інтеграла по іншому називають інтегруванням функції.

Таким чином, операція інтегрування функції є оберненою до операції диференціювання. Щоб перевірити чи вірно проінтегрована функція слід продифереціювати результат інтегрування. Якщо у підсумку дістанемо підінтегральну функцію, то інтеграл знайдено правильно. Отже, по таблиці похідних функції можна записати таблицю інтегралів.

Властивості невизначеного інтеграла:

1.

2.

3.

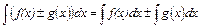
4.

Таблиця невизначених інтегралів:

1. .

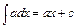2. 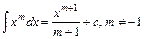. Зокрема, , , .

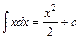3. .

4. .

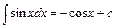5. .

6. .

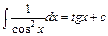7. .

8. . Зокрема .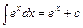

9. 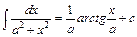. Зокрема, .

10. 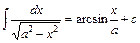. Зокрема, .

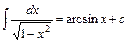11. .

12. .

13. .

14. .

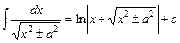Методи інтегрування:

· табличний – використовують табличні інтеграли, властивості інтегралів та властивості підінтегральної функції;

· заміни змінної під знаком інтеграла (метод підстановки) – полягає у використанні формули

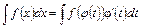, (2)

де , ,

або тієї ж формули у зворотному напрямку:

, (2’)

де , .

Якщо функції 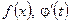неперервні, то рівності (2) і (2’) виконуються завжди. Заміна змінної є ефективною, якщо інтеграли справа у цих рівностях є простішим від відповідних інтегралів зліва. Якщо ж інтеграл справа ускладнився, то слід шукати іншу заміну, або відмовитись від цього методу інтегрування.

· інтегрування частинами – базується на використанні формули

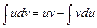, (3)

де .

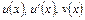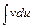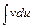У цій інтегральній тотожності підінтегральний вираз представлено у вигляді добутку . Якщо функції є неперервними, тотожність (3) виконується завжди. Метод інтегрування частинами є ефективним лише у випадку, коли інтеграл справа у цій рівності є простішим за інтеграл зліва . Якщо є інтеграл став складнішим, то розбиття підінтегрального виразу на добуток і застосування формули (3) не приводить до результату. У цьому випадку слід позначити за u та dv інші частини підінтегрального виразу, або відмовитись від цього методу інтегрування.

Є функції, для інтегрування яких можна застосовувати наперед відомий метод інтегрування, а є такі, для інтегрування яких невідомо, який метод застосовувати. У цьому випадку застосовують один із перелічених методів. Не отримавши результату застосовують інший, або здійснюють перетворення над підінтегральною функцією і т.п.

Дата добавления: 2015-05-23