
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади. 1. Обчислити інтеграли методом безпосереднього інтегрування
|
|
|
|
1. Обчислити інтеграли методом безпосереднього інтегрування
а)  , б)
, б) 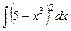 , в)
, в)  , г).
, г). 
Розв'язання. а. За формулою 2 з таблиці невизначених інтегралів для  дістаємо
дістаємо
 ;
;
б. Розкриємо дужки під знаком інтеграла і за формулою для  визначаємо
визначаємо
 ;
;
в. Згідно з властивостями 3 і 4 невизначеного інтеграла і табличними інтегралами маємо
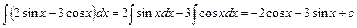 .
.
г. За формулою 9 із таблиці невизначених інтегралів для  дістаємо
дістаємо
 .
.
2. Обчислити інтеграл методом заміни змінної під знаком інтеграла (підстановки) та здійснити перевірку правильності знаходження інтеграла.
а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
Розв'язання. а. Здійснимо заміну змінної  . Тоді
. Тоді 
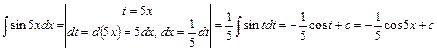 .
.
Щоб перевірити, чи правильно знайдено інтеграл знайдемо похідну від результату інтегрування:
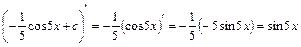 .
.
Отже, інтеграл знайдено правильно.
б. У цьому прикладі застосуємо перетворення над підінтегральною функцією 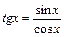 , а потім здійснимо заміну змінної
, а потім здійснимо заміну змінної  :
:
 .
.
Перевірка:  . Інтеграл знайдено правильно.
. Інтеграл знайдено правильно.
в. 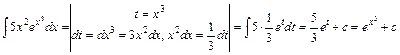 .
.
Перевірка:  .
.
г. 
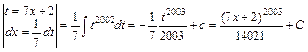 .
.
Перевірка: 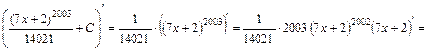
 .
.
д. Врахувавши, що  та
та  , здійснимо заміну змінної під знаком інтеграла t= arctg x:
, здійснимо заміну змінної під знаком інтеграла t= arctg x:
 .
.
Перевірка:  .
.
е. Для цього інтеграла слід врахувати, що  та здійснити заміну t= sin x:
та здійснити заміну t= sin x:
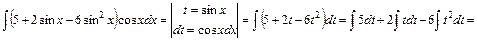
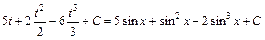 .
.
Перевірка: 
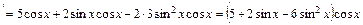 .
.
3. Обчислити інтеграл методом інтегрування за частинами:
а)  , б)
, б)  , в)
, в)  , г)
, г) 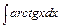 ,
,
д)  , е)
, е)  .
.
Розв'язання. а. Щоб скористатись базовою формулою (5.3) позначимо:  ,
,  . Тоді
. Тоді  ,
,  . Підставивши
. Підставивши  ,
,  і
і  у праву частину базової формули дістанемо
у праву частину базової формули дістанемо

 .
.
Якщо ж позначити:  ,
,  , то дістанемо
, то дістанемо  ,
,  , та
, та
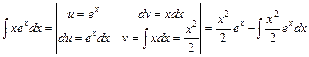 .
.
Інтеграл справа  став складнішим ніж інтеграл зліва
став складнішим ніж інтеграл зліва  . Тому в методі інтегрування частинами підінтегральний вираз
. Тому в методі інтегрування частинами підінтегральний вираз  недоцільно представляти у вигляді добутку udv, якщо
недоцільно представляти у вигляді добутку udv, якщо  та
та  .
.
б. Позначимо:  ,
,  . Тоді
. Тоді  ,
,  . Підставивши
. Підставивши  ,
,  і
і  у праву частину базової формули (5.3) дістанемо
у праву частину базової формули (5.3) дістанемо
 ;
;
в)  ;
;
г) У цьому прикладі застосовується спочатку метод інтегрування частинами, а потім метод підстановки:

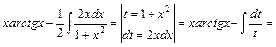
 .
.
д) У розглядуваному випадку інтегрування за частинами потрібно застосувати кілька разів:


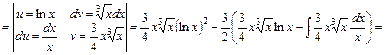

 .
.
е) 

 .
.
Завдання для самостійного розв'язання
1. Обчислити невизначений інтеграл методом безпосереднього інтегрування:
а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  е)
е)  .
.
2. Обчислити невизначений інтеграл методом заміни:
а)  , б)
, б) 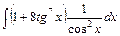 , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е) 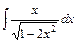 , ж)
, ж)  .
.
3. Обчислити невизначений інтеграл методом інтегрування за частинами:
а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
4. Обчислити невизначений інтеграл, вибравши один із методів інтегрування:
а) 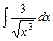 , б)
, б)  , в)
, в)  , г)
, г)  ,
,
д) 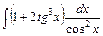 , е)
, е)  , ж)
, ж) 
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 2501; Нарушение авторских прав?; Мы поможем в написании вашей работы!