Формулировка

Определение скорости, индуцированной вихрем. Формула Био-Савара. Частные случаи – отрезок, бесконечные и полубесконечные вихри.

Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.

Пусть постоянный ток 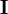течёт по контуру γ, находящемуся в вакууме, 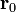— точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)

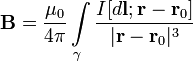
Направление 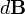перпендикулярно 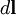и 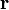, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление 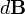, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора 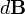определяется выражением (в системе СИ)

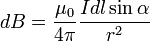
Векторный потенциал даётся интегралом (в системе СИ)

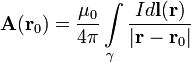
Уравнение неразрывности.

В гидродинамике уравнение непрерывности называют уравнением неразрывности. Оно выражает собой закон сохранения массы в элементарном объеме, то есть непрерывность потока жидкости или газа. Его дифференциальная форма

,

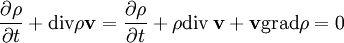где 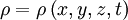— плотность потока жидкости (или газа), 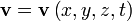— вектор скорости жидкости (или газа) в точке с координатами 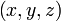в момент времени .

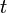Вектор 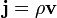называют плотностью потока жидкости. Его направление совпадает с направлением течения жидкости, а абсолютная величина определяет количество вещества, протекающего в единицу времени через единицу площади, расположенную перпендикулярно вектору скорости.

Для несжимаемых жидкостей 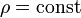. Поэтому уравнение принимает вид

,

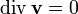из чего следует соленоидальность поля скорости.

Уравнение движения вязкого газа (Навье-Стокса).

Уравне́ния Навье́ — Сто́кса — система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Луи Навье и британского математика Джорджа Стокса.

Система состоит из двух уравнений:

• уравнения движения,
• уравнения неразрывности.

В векторном виде для несжимаемой жидкости они записываются следующим образом:

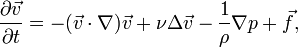
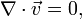
где — оператор Гамильтона, 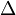— оператор Лапласа, 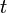— время, 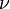— коэффициент кинематической вязкости, 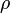— плотность, 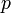— давление, 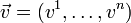— векторное поле скоростей, 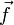— векторное поле массовых сил. Неизвестные 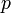и 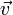являются функциями времени 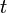и координаты 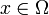, где 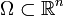, 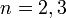— плоская или трехмерная область, в которой движется жидкость. Обычно в систему уравнений Навье-Стокса добавляют краевые и начальные условия, например

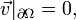
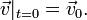
Иногда в систему уравнений Навье — Стокса дополнительно включают уравнение теплопроводности и уравнение состояния.

При учёте сжимаемости уравнение Навье — Стокса принимает следующий вид:

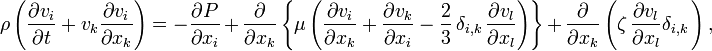
где 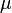— коэффициент динамической вязкости, 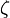— «вторая вязкость».

В анализе решений уравнений заключается суть одной из открытых проблем, за решение которых Математический институт Клэя назначил премию в 1 млн долларов США. Необходимо доказать или опровергнуть существование глобального гладкого решения задачи Коши для трехмерных уравнений Навье — Стокса. Нахождение общего аналитического решения системы Навье — Стокса для пространственного или плоского потока осложняется тем, что оно нелинейное и сильно зависит от начальных и граничных условий.

Также ряд коммерческих фирм, например Боинг, назначили свои премии.^{[ источник не указан 232 дня ]}

До сих пор решения этих уравнений найдены лишь в некоторых частных случаях. В настоящее время существует несколько ситуаций (обусловленных простой геометрией), которые решены в аналитическом виде. В остальных случаях используется численное моделирование.

Некоторые точные решения:

1. Стационарные течения в простых каналах (течение Пуазейля, течение Тейлора-Куэтта и пр.)
2. Солитоны и нелинейные волны. Обычный солитон может являться решением системы при очень сложных граничных условиях. Впервые он наблюдался экспериментально в канале инженером Скотом Расселом.
3. Решение, которое существует конечное время (так называемые режимы с обострением, blow-up). Капнув каплю на поверхность воды, можно наблюдать всплеск, который существует конечное время, как и кольцевой вихрь ядерного взрыва. Гипотеза об этом выдвинута Jean Leray в 1933 г. Он предположил, что в жидкости турбулентность (хаос) образуется благодаря образованию точек или вихревой нити, на которой некоторая компонента скорости становится бесконечной.
4. Звуковые колебания. При малой амплитуде волн они также становятся решением. Нелинейные члены уравнения можно отбросить, так как они не влияют на решение. Решением являются гармонические функции синуса или косинуса, то есть звуковые колебания, которые мы слышим.

Дата добавления: 2015-05-23