Формула Стокса

Циркуляция вектора поля.

Пусть рассматривается векторное поле какой-то величины 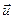. Циркуляцией вектора 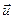вдоль контура L называют криволинейный интеграл вида

(1.12)

Иногда этот интеграл интерпретируется как «работа» векторного поля вдоль контура L. Если циркуляция векторного поля вдоль замкнутого пути (контура) равна нулю, то поле называют потенциальным.

Эта формула позволяет преобразовать криволинейный интеграл вдоль замкнутой пространственной кривой в поверхностный интеграл по поверхности, натянутой на эту кривую, т. е.

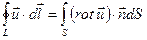(1.13)

т. е. циркуляция вектора поля вдоль контура равна потоку вихря через поверхность, ограниченную этим контуром.

Формула Остроградского – Гаусса.

Это соотношение, часто называемое преобразованием Остроградского – Гаусса, связывает поверхностный интеграл по замкнутой поверхности с интегралом по объему, ограниченному этой поверхностью

(1.15)

Формула показывает, что поток векторного поля через замкнутую поверхность равен интегралу от дивергенции поля по объему, ограниченному этой поверхностью.

В механике жидкости широко используется формула, являющаяся следствием формулы Остроградского – Гаусса для скалярного поля

(1.16)

где – какая-то скалярная функция.

Дата добавления: 2015-05-23