Уравнение энергии

Уравнение движения вязкой несжимаемой жидкости

(уравнение Навье—Стокса)

Это уравнение получается путем подстановки выражений (3.5) в (3.9'). После преобразований с учетом (2.13') и (1.3) получим

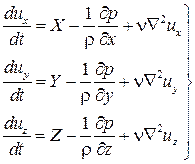(3.10’)

где 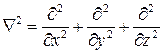- оператор Лапласа.

Умножив построчно выражения (3.10') на 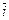, и и про­суммировав их, получим уравнения Навье—Стокса в вектор­ной форме записи:

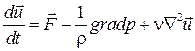, (3.10)

где ; ,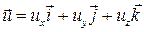

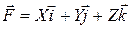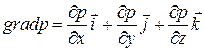(3.11)

В уравнении (3.10) слагаемое du/dt характеризует инер­ционные силы, 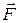— массовые силы силового поля, в котором движется жидкость, 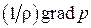— поверхностные силы — силы давления и 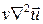— поверхностные силы — силы вязкостного трения.

При формулировке конкретных задач важным моментом является формулирование краевых условий. Одно из важных граничных условий — это условие прилипания на границе с твердой непроницаемой поверхностью, скорость жидкости равна скорости поверхности тела.

Уравнение энергии составляется на основе закона сохранения энергии: изменение энергии Е жидкости в отсутствие теплообмена с окружающей средой может произойти только за счет работы внешних сил:

dE = dA = Ndt

или

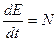, (3.12)

где N — мощность, затрачиваемая внешними силами.

Для гомогенной жидкости в отсутствие изменения агрегатного состояния

,

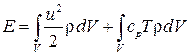где c_p — теплоемкость жидкости при температуре Т; V — произвольный объем движущейся жидкости. Тогда для несжимаемой жидкости

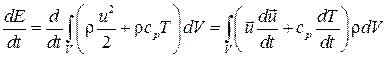. (3.13)

Величину N можно представить в виде

N=N_m+N_s, (3.14)

где N_m — мощность внешних массовых сил

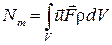; (3.15)

N_S — мощность внешних поверхностных сил

.

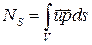С учетом теоремы о кратных интегралах можно записать

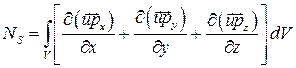. (3.16)

Подставим выражения (3.13) — (3.16) в (3.12), просуммируем подынтегральные функции всех входящих в (3.12) вы­ражений. Как и ранее, сумма этих функций равна нулю, так как не сделано было каких-либо ограничений на объем V. Получим после простейших преобразований

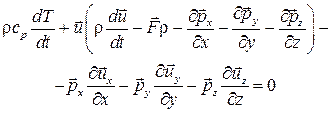.(3.17)

Выражение в скобках равно нулю (см. (3.9)). Раскроем скалярное произведение последних трех слагае­мых. Тогда (3.17) примет вид

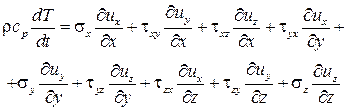
После подстановки в (3.17) выражений (3.5) окончатель­но найдем

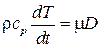, (3.18)

где

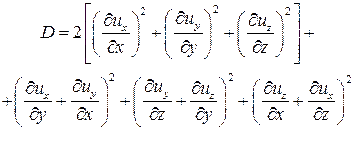
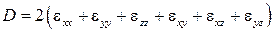
Функция D называется диссипативной функцией.

Произведение m D характеризует ту часть механической энергии, которая рассеялась, или диссипировалась, в едини­це объема жидкости, т. е. перешла в тепловую (внутреннюю) энергию.

Дата добавления: 2015-05-23