
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы кинематики жидкости
|
|
|
|
Скорость жидкости может быть задана двумя способами. Первый из них (метод Лагранжа), наиболее естественный, предполагает известными траектории движения каждой жидкостной частицы, имеющей в начальный момент времени координаты r0 или (а, b, с); 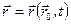 или х=х(а, b, с, t); у=у(а, b, с, t); z=z(a, b, с, t). Переменные
или х=х(а, b, с, t); у=у(а, b, с, t); z=z(a, b, с, t). Переменные  или а, b, с называются переменными Лагранжа. В этом случае мгновенную скорость можно вычислить так:
или а, b, с называются переменными Лагранжа. В этом случае мгновенную скорость можно вычислить так:
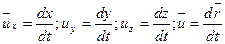
Отметим, что этот метод описания движения жидкости не получил широкого применения из-за сложности получаемых уравнений движения.
Второй метод (метод Эйлера) заключается в непосредственном описании поля скоростей в пространстве и времени:  или ux=ux(x,y,z,t); uy=uy(x,y,z,t); и
или ux=ux(x,y,z,t); uy=uy(x,y,z,t); и 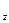 = uz(x, у, z, t).
= uz(x, у, z, t).
Этот метод получил преимущественное применение.
 Движение называется установившимся или стационарным, если скорость в каждой точке пространства не изменяется во времени (например, истечение жидкости из отверстия в днище сосуда при постоянном уровне жидкости). Если же скорость изменяется во времени, то движение называется неустановившимся или нестационарным.
Движение называется установившимся или стационарным, если скорость в каждой точке пространства не изменяется во времени (например, истечение жидкости из отверстия в днище сосуда при постоянном уровне жидкости). Если же скорость изменяется во времени, то движение называется неустановившимся или нестационарным.
Линия тока — это линия, в каждой точке которой в данный момент времени вектор скорости и направлен по касательной (рис. 2.1). Из определения следует, что 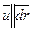 , т. е. их векторное произведение
, т. е. их векторное произведение  , или так как
, или так как  , a
, a 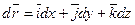 , то
, то 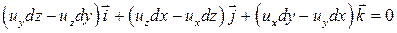 , или
, или
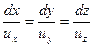 (2.1)
(2.1)
Уравнение (2.1)—это дифференциальное уравнение линии тока.
Траектория — линия, по которой материальная точка перемещается в пространстве во времени. За время dt точка пройдет путь 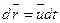 . В проекции на оси координат
. В проекции на оси координат  или
или
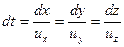 (2.2)
(2.2)
Уравнение (2.2) — дифференциальное уравнение траектории по форме совпадает с уравнением для линии тока (2.1). Однако решения их различны: при нахождении уравнения линии тока интегрирование уравнения необходимо проводить для данного момента времени t= const. Линия тока и траектория совпадают при установившемся движении жидкости.
Трубка тока. Через каждую точку произвольного контура l проведем линии тока (рис. 2.2). Полученная трубчатая поверхность называется трубкой тока. Если контур l мал, то трубка тока называется элементарной.
Объемный расход жидкости через произвольное сечение ds снормалью  элементарной трубки тока (рис. 2.3) вычислим из простых рассуждений: объем жидкости, протекший
элементарной трубки тока (рис. 2.3) вычислим из простых рассуждений: объем жидкости, протекший


через сечение ds за время dt, равен объему цилиндра 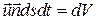 ,т. е. расход
,т. е. расход
 (2.3)
(2.3)
где ип — проекция 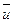 на нормаль
на нормаль  ;
;  — площадь сечения, перпендикулярная линиям тока, или «живое сечение».
— площадь сечения, перпендикулярная линиям тока, или «живое сечение».
По аналогии массовый расход жидкости в элементарной трубке тока
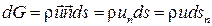 (2.4)
(2.4)
Расход жидкости через произвольную площадку s можно вычислить, просуммировав расходы по элементарным пронизывающим ее трубкам, т. е. объемный расход
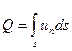 (2.5’)
(2.5’)
массовый расход
 (2.5)
(2.5)
Размерность: [Q] = м3/c; [G]=кг/с.
Средняя расходная скорость v в живом сечении sn связана с объемным расходом соотношением
Q = vsn. (2.6)
Ускорение при движении жидкости вычисляется по формуле

Если известно поле скоростей (по методу Эйлера), то при вычислении ускорения следует помнить, что и—и (х, у, z, t). Тогда
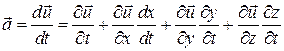
а переменные dx, dy,dz не произвольны, а связаны между собой уравнением траектории (2.2), т. е.
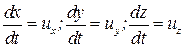
Итак,
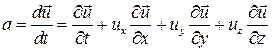 (2.7)
(2.7)
Составляющая ускорения 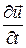 — называется локальным ускорением, она характеризует изменение скорости в данной точке пространства. Очевидно, что при установившемся движении
— называется локальным ускорением, она характеризует изменение скорости в данной точке пространства. Очевидно, что при установившемся движении 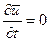 . Сумма слагаемых
. Сумма слагаемых  — называется конвективным ускорением, она характеризует изменение скорости в данный момент времени вдоль линии тока. Конвективное ускорение всегда равно нулю в прямых каналах (или трубках тока) постоянного сечения при течении несжимаемой жидкости.
— называется конвективным ускорением, она характеризует изменение скорости в данный момент времени вдоль линии тока. Конвективное ускорение всегда равно нулю в прямых каналах (или трубках тока) постоянного сечения при течении несжимаемой жидкости.
В проекциях на оси х, у, z уравнение (2.7) примет вид:
 (2.8)
(2.8)
Уравнение неразрывности — это уравнение материального баланса. Зафиксируем в пространстве произвольный объем V (рис. 2.4). Масса жидкости в объеме 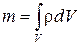 .
.
Изменение массы во времени
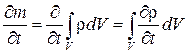 (2.9)
(2.9)
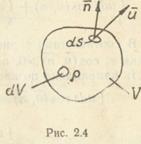 может произойти только за счет притока жидкости, который равен суммарному массовому расходу жидкости через поверхность s объема V.
может произойти только за счет притока жидкости, который равен суммарному массовому расходу жидкости через поверхность s объема V.
Если 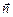 — внешняя нормаль к поверхности ds, то с учетом (2.5) приток
— внешняя нормаль к поверхности ds, то с учетом (2.5) приток
 (2.10)
(2.10)
Приравняв выражения (2.9) и '(2.10), получим уравнение неразрывности в интегральной форме:
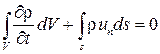 (2.11)
(2.11)
Слагаемое (2.10) с учетом теоремы о кратных интегралах (теоремы Остроградского-Гаусса) можно преобразовать к виду

Подставим это выражение в (2.11). Просуммируем подынтегральные функции. Получим
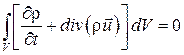
Поскольку предел интегрирования V произволен, то последний интеграл может быть равен нулю только при условии, что
 (2.12)
(2.12)
Уравнение (2.12)—это уравнение неразрывности в дифференциальной форме.
Для несжимаемой жидкости r=const; 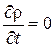 и уравнение примет вид
и уравнение примет вид
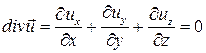 (2.13)
(2.13)
или
 (2.13’)
(2.13’)
Для потока несжимаемой жидкости в трубке тока уравнение (2.11) принимает вид
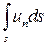
или
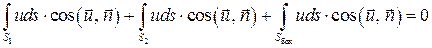
В соответствии с рис. 2.2 в сечении s 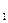 cos(
cos( ) <0, в сечении s2 cos(
) <0, в сечении s2 cos( ,
,  )>0, а на поверхности s6 cos(
)>0, а на поверхности s6 cos( ,
,  )=0 (скорость направлена по касательной к sб). Поэтому
)=0 (скорость направлена по касательной к sб). Поэтому
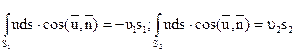
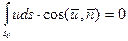
и уравнение неразрывности для трубки тока
 (2.14)
(2.14)
Скорость деформации. Скорость жидкости в точке, отстоящей от точки А (рис. 2.5) на расстоянии dr, можно вычислить по формуле
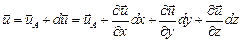
или
 (2.15)
(2.15)
Различие скоростей возникает из-за:
а) растяжения жидкостного элемента (рис. 2.6, а) — линейной деформации;
б) угловой деформации (рис. 2.6, б);
в) вращения элемента без деформации (рис. 2.6, в) — 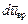
Следовательно, различие скоростей в результате деформации жидкостного элемента
 (2.16)
(2.16)
Прежде чем приступить к расчету 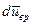 по известному полю скоростей u=u(x, y, z), вспомним, каков кинематический смысл частных производных.
по известному полю скоростей u=u(x, y, z), вспомним, каков кинематический смысл частных производных.
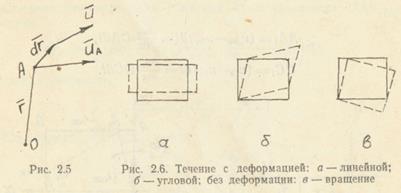
1. Кинематический смысл дих/дх.
Пусть в системе координат, связанной с точкой О жидкости, за время dt точка А переместится и займет положение А (рис. 2.7). Тогда удлинение отрезка АА1=(иАх — u 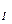
 )dt, и, так как для бесконечно малого отрезка ОА
)dt, и, так как для бесконечно малого отрезка ОА
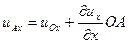 , то
, то 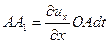 .
.
Скорость удельного удлинения отрезка ОА или скорость линейной деформации вдоль оси х
 (2.17)
(2.17)
По аналогии 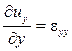 и
и 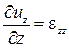 – скорости линейных деформаций вдоль осей у и z
– скорости линейных деформаций вдоль осей у и z
соответственно.
Уравнение неразрывности несжимаемой жидкости (2.13'), представленное в виде

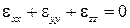
говорит о неизменности объема элемента жидкости при его линейной деформации.
2. Кинематический смысл ¶ их/ ¶ z и ¶ иz/ ¶ x.
Пусть за время dt точка А переместится в А1, В — b1, C—C1 (рис. 2.8).
Поскольку
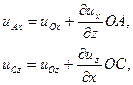
то

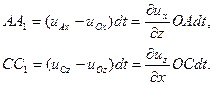
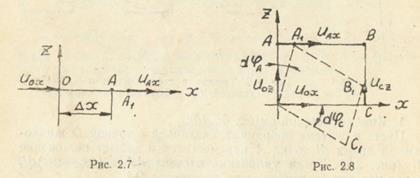
Угол поворота линии ОА  , а линии ОС
, а линии ОС 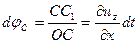 , т. e. частные производные dux/dz и ди
, т. e. частные производные dux/dz и ди 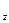 /дх равны угловым скоростям вращения линий ОА и ОС соответственно.
/дх равны угловым скоростям вращения линий ОА и ОС соответственно.
Суммарная угловая деформация прямоугольника ОАВС
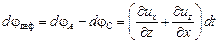 .
.
Скоростью угловой деформации в плоскости х — z называется величина

Т.е.
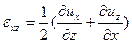 (2.18)
(2.18)
По аналогии, рассмотрев угловые деформации в плоскостях ху и уz, найдем
 (2.18’)
(2.18’)
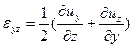 (2.18’’)
(2.18’’)
Среднее значение угла поворота прямоугольника ОАВС
| а угловая скорость |
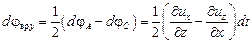
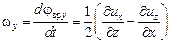 (2.19)
(2.19)
По аналогии нетрудно найти
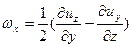 (2.19’)
(2.19’)
 (2.19’’)
(2.19’’)
Вычислим duвр, входящее в (2.16)
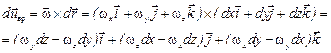
Подставим найденное выражение в (2.16) и запишем его в проекции на ось х:

С учетом (2.19') и (2.19"), а также (2.17), (2.18) и (2.18') после преобразований получим
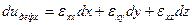
По аналогии


Матрица, составленная из девяти компонентов скоростей линейных и угловых деформаций называется тензором скоростей деформаций S.
 (2.20)
(2.20)
Она симметрична относительно главной диагонали, т. е. 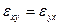 ,
, 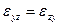 ,
, 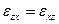 , и применительно к несжимаемой жидкости независимо от ориентации координатных осей
, и применительно к несжимаемой жидкости независимо от ориентации координатных осей
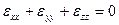
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 658; Нарушение авторских прав?; Мы поможем в написании вашей работы!