Уравнение Бернулли для плоского установившегося течения

Уравнение движения идеальной жидкости (уравнение Эйлера)

ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ

Закон Архимеда

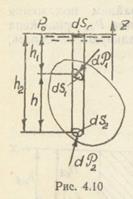
Если пронизать тело, погруженное в жидкость, вертикаль­ным цилиндром с основанием ds_г, то на площадки ds₁ и ds₂, отсекаемые на поверхности тела (рис. 4.10), действуют соответственно гидростатические силы, вертикальные составляю­щие которых

dP_1z=rgh₁s_r

и

dP_2z=rgh₂s_r.

Результирующая сила направлена вверх и равна

dP_z =dP_2z—dP_lz= 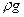(h₂—h₁)ds_г=rgdW,

где dW — объем тела, отсекаемый эле­ментарным цилиндром.

Просуммировав силы по всей поверх­ности тела, найдем, что

P_z=rgW,

где W — объем тела, погруженного в жидкость.

Поскольку идеальная жидкость имеет v =m=0, то урав­нения (3.10) и (3.10') примут соответственно вид

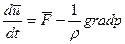(5.1)

и

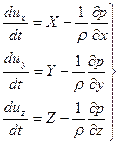(5.1’)

Уравнения (5.1) и (5.1')—это уравнения Эйлера для движущейся идеальной жидкости.

Движение называется плоским, если линии тока лежат в плоскости и не изменяют своей конфигурации при парал­лельном переносе этой плоскости.

Если, например, линии тока лежат в плоскости xz, то u_y=0 и система уравнений (5.1') примет вид

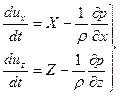(5.2)

При установившемся движении 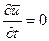и для расчета ускорений в (5.2) можно применить зависимости (см. уравнения 2.8):

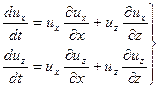(5.3)

Выясним, при каких условиях уравнения (5.2) можно представить в виде полного дифференциала некоторой функции, т. е. установить их общее решение. Для этого умножим построчно уравнения (5.2) на dx и dz и сложим. Получим

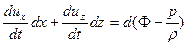, (5.4)

где выражение dФ = Xdx+Zdz справедливо в случае, когда поле массовых сил потенциально.

Подставим в (5.4) выражения (5.3). Прибавим к левой части и вычтем из нее слагаемые 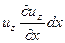и 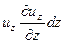. После некоторых преобразований получим

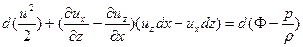. (5.5)

Итак, искомое условие выполняется тогда, когда второе слагаемое в (5.5) равно нулю, т. е. в двух случаях:

1. Сомножитель u_zdx — u_xdz=0 или 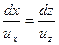, т. е. в случае, когда интегрирование (5.5) приводится вдоль линии то­ка (см. уравнение 2.1).

2. Сомножитель 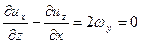(см. уравнение (2.19)), т. е. отсутствует вращательное движение жидкост­ных частиц (такое движение называется безвихревым или потенциальным).

При выполнении условий 1 или 2 уравнение (5.5) можно записать в виде

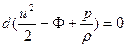, (5.6)

т. е. в идеальной жидкости при течении вдоль линии тока или в случае безвихревого движения во всем пространстве выполняется условие

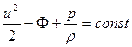. (5.7)

Для гравитационного поля и при вертикальном располо­жении оси z Х=0; Z=— g, т. е. dФ=Xdx+Zdz= — gdz или Ф = — gz+C₁.

С учетом этого выражения уравнение (5.7) можно запи­сать в виде

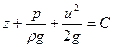. (5.8)

Уравнение (5.8) — это уравнение Бернулли. Поясним энергетический смысл уравнения Бернулли.

С учетом пояснений, данных при анализе уравнения (4.8), z — удельная потенциальная энергия положения, p/(pg) — удельная потенциальная энергия давления. В уравнении (5.8) третье слагаемое 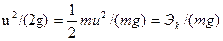, т. е. представляет собой отношение кинетической энергии к весу жидкостной частицы, или удельную кинетическую энергию. Следовательно, сумму всех трех слагаемых можно назвать удельной полной энергией:

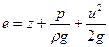. (5.9)

В такой интерпретации уравнение (5.8) — это уравнение сохранения механической энергии.

Дата добавления: 2015-05-23