Равномерное ламинарное течение в плоском канале

Ламинарное безнапорное течение Куэтта

Это установившееся течение жидкости между двух парал­лельных пластин под действием движения одной из них (см. рис. 1.1). В уравнениях (3.10') u_z=u_y=0; X=0; =0; =0. Следовательно, уравнение движения в проекции на ось х примет вид

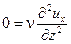
Интегрируем

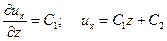
Граничное условие: при z=0, 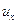=0, отсюда С₂=0; при

z= u_x = u₀, тогда С₁= .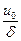

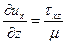Итак, распределение скоростей в зазоре, как ранее и предполагалось, линейно и подчиняется зависимости u_x=u₀z/ . Из (3.5) следует, что и так как 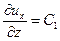= const, то ясно, что при течении Куэтта = const (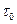 — касательное напряжение на стенке канала).

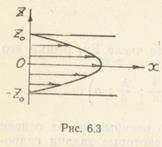
При установившемся течении жидкости вдоль оси (рис. 6.3) в горизонтальном канале u_y = u_z=0;X=0;du_x/dt=0.

Уравнение движения (3.21') в проекции на ось х примет вид

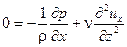(6.9)

На ось z 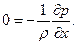т.е. в живом сечении р =С(х) — pgz, и др/дх не зависит от z. Проинтегри­руем(6.9) дважды по z. С учетом

(1.3) и граничных условий: при z 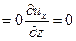; при z=z₀ и_х=0 получим уравнение для рас­чета распределения скоростей

Максимальная скорость (при z=0): u _m =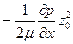

Вычислим расход жидкости в канале при ширине его В:

Средняя расходная скорость ,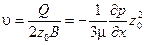

Откуда

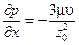(6.10)

Перепад давлений в канале длиной l найдем, проинтегри­ровав (6.10) по х:

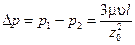(6.11)

где р₁ и p₂ — давление в начале и конце канала соответ­ственно. Уравнение (6.11)—искомая расчетная зависимость. При решении практических задач для вычисления потерь давления при течении жидкости в горизонтальных каналах часто применяется уравнение Дарси—Вейсбаха:

(6.12)

С учетом того, что для плоского канала d₃ = 4z₀, прирав­няв (6.11) и (6.12), легко найти выражение для расчета ко­эффициента гидравлического трения X = 96/Re, справедливого для ламинарного течения.

Дата добавления: 2015-05-23