Решение задач гидродинамики методом теории подобия

Уравнение турбулентного течения несжимаемой жидкости (уравнение Рейнольдса)

При решении практических задач обычно бывают заданы средние во времени значения скоростей 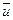и напряжений 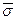, 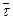. Уравнение движения, выраженное через 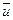и 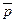, было выведе­но Рейнольдсом. В качестве исходных возьмем уравнения движения в напряжениях (3.9'). Преобразования выполним для первого из них.

С учетом (2.8) и (2.13) ускорение можно предста­вить в виде

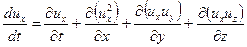(6.1)

Истинные значения скоростей и напряжений с осредненными связаны зависимостями:

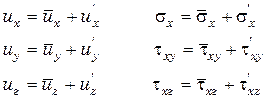(6.2)

Здесь и_х', и_у', u_z', 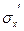, , 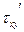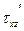- пульсационные состав­ляющие.

Подставим уравнения (6.1) и (6.2) в (3.9') и проведем операцию сглаживания (осреднения) функций по правилам:

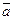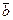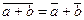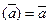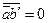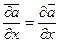если а = + a ' и b= +b', то ; ; ; =0; После

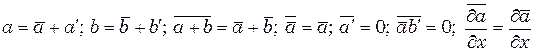
преобразований получим

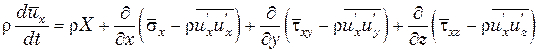(6.3)

Итак, при турбулентном течении жидкости в результате пульсаций скоростей возникают дополнительные или турбу­лентные напряжения. Аналогичные только что приведенным преобразования со всеми уравнениями (3.9') позволяют выявить шесть независимых компонентов турбулентных на­пряжений:

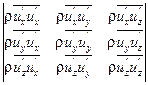(6.4)

Система, состоящая из уравнения Рейнольдса, уравнений (2.13') и (3.5), которые после сглаживания не претерпят из­менений, не замкнута. Для замыкания ее необходимы еще шесть уравнений.

6.3. О моделировании в гидромеханике

Два процесса подобны, если описываются тождественными уравнениями с тождественными граничными условиями и протекают в геометрически подобной обстановке. Зная условия подобия, можно исследовать модельный аппарат, машину, а потом перенести результаты испытаний на реальный проектируемый объект. Для выявления условий гидромеханического подобия преобразуем уравнение Навье—Стокса (3.10') к безразмерному виду.

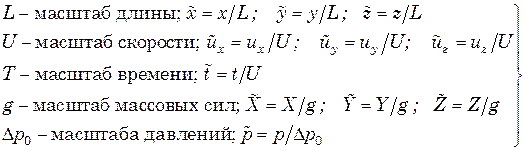(6.5)

Здесь величины, отмеченные волнистой линией, безразмер­ные. Подставим (2.8) в (3.10'). С учетом (6.5) первое из уравнений (3.10') можно представить в виде (после вынесе­ния масштабов из-под знаков дифференциала умножим все слагаемые на L/U²)

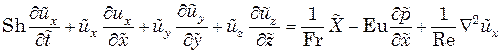, (6.6)

где .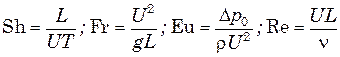

Безразмерные коэффициенты Sh, Fr, Eu, Re называются числами подобия (иногда — критериями подобия) и носят имена ученых: Sh— число Струхаля; Fr—число Фруда; Еu — число Эйлера; Re — число Рейнольдса. Равенства чисел подобия в уравнении (6.6) и геометрическое подобие модели и объекта достаточно для обеспечения подобия гидромеха­нических процессов.

Поскольку каждое из слагаемых уравнения Навье—Стокса характеризует одну из сил, действующих в жидкости, то числа подобия характеризуют их отношения. Так,

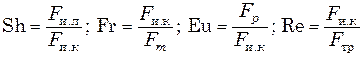,где

F_и._л — сила инерции, вызванная локальным ускорением;

F_и.к — сила инерции, вызванная конвективным ускоре­нием;

F_м— массовая сила;

F_тр — сила вязкостного трения;

Fр — сила давления.

Полную модель для объекта не всегда удается получить.

Например, пусть L ₀ /L _м =10² (индексы: о – объект; м – модель). Тогда из равенства чисел Фруда U ₀² / (gL ₀) = U _м² / (gL _м)следует, что U ₀ /U _м = (L ₀/ L _м)^0,5=10; из равенства чисел Рейнольдса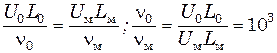

испытания модели надо проводить в среде, вязкость которой значительно ниже вязкости среды объекта, что не всегда удается реализовать.

При интегрировании дифференциальных уравнений в оп­ределенных пределах решение всегда содержит лишь ту или иную комбинацию коэффициентов уравнения и граничные условия.

Поясним это на легко решаемом примере. Дано уравне­ние 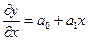и начальное условие при x=x₀ у=у₀. Вычислить y₁ при х =x_1. После введения масштабов x₀ и у₀ и приведения уравнения к безразмерной форме нетрудно най­ти, что решение задачи имеет вид

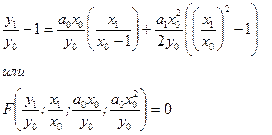
По аналогии можно утверждать, что и решение уравне­ния Навье—Стокса можно записать F(Sh; Fr; Eu; Re; Г₁; Г₂;...)=О, где Г₁; Г₂ — отношения различных размеров объ­екта к масштабу L, определяющие его геометрию (геометри­ческие симплексы).

Покажем, что применение уравнения движения в безраз­мерном виде существенно сокращает объем эксперименталь­ных исследований, необходимых для уточнения вида искомой функции. Рассмотрим несколько примеров:

а) установившееся ламинарное течение в жидкости в го­ризонтальной трубе. В качестве масштабов при решении этой задачи можно принять L = d, U=v (d — диаметр тру­бы; v — средняя расходная скорость). Поскольку 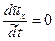и 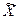=0, то уравнение (6.6) существенно упростится и его можно привести к виду

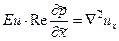
т. е. получим уравнение с одним коэффициентом Eu*Re. Ре­шение следует искать в виде F(Eu*Re; l/d=0), где l — дли­на трубы, или Eu*Re=f(l/d). Физически очевидно, что

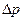~l, т.е. f(l/d) =C 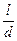и расчетное уравнение содержит только один неизвестный коэффициент С:

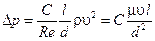(6.7)

б) установившееся турбулент­ное течение в горизонтальной трубе. Если подставить уравнение (3.5) в (6.3) и привести последнее к безразмерному виду, то при

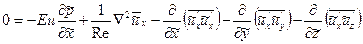
Это уравнение содержит два независимых коэффициента Еu и Re и его решение следует искать в виде (Eu; Re; 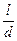)=0

или Eu=f(Re) 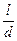, или

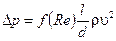(6.8)

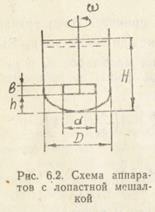
в) установившийся турбулентный режим перемешивания жидкости в аппарате с мешалкой (рис. 6.2). В отличие от предыдущей задачи в уравнении сохраняется слагаемое 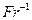X и решение следует искать в виде

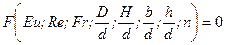, (6.9)

где n — число лопастей.

Выберем масштабы: L = d; 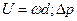— средний пере­пад давлений на лопасти. Сила F, действующая на n лопа­стей, пропорциональна 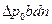, а мощность N на перемеши­вание жидкости N~F 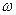d, т. е.

~

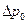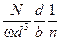
С учетом выбранных масштабов числа подобия примут вид

Подставив в (6.9) преобразованное число Еu, решим его относительно k_N

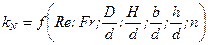
Вид этой зависимости чаще всего раскрывают на основе экспериментальных исследований. Некоторые задачи гидро­механики удается решить точными методами. Рассмотрим простейшие из них.

Дата добавления: 2015-05-23