Плоские потенциальные течения

При изучении плоских течений как реальной, так и иде­альной жидкости, удобно ввести функцию тока y, которая связана со скоростями и_х и u_z соотношениями

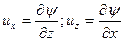. (5.10)

Соотношения (5.10) всегда удовлетворяют уравнению не­разрывности, а уравнения движения (5.2) преобразуются в систему двух уравнений с двумя скалярными переменными p и y.

Функция, тока y=const на линии тока. Это легко увидеть, если подставить (5.10) в уравнение для линии тока u_xdz — u_zdx=0:

.

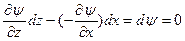Ранее было показано, что при плоском безвихревом или потенциальном течении идеальной жидкости, когда выпол­няется условие

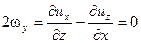, (5.11)

интеграл уравнения движения имеет вид (5.8) — уравнение Бернулли, которое взаимосвязывает две величины: р и u. По­этому задача сводится к интегрированию уравнения нераз­рывности.

При выполнении условия (5.11) существует такая функ­ция y, что

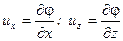. (5.12)

Чтобы убедиться в этом, подставьте (5.12) в (5.11). Функция j называется потенциалом скорости, а течение при выполнении условия (5.11)—потенциальным.

Подстановкой уравнений (5.12) в уравнение неразрывности (2.13') получим уравнение Лапласа:

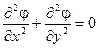, (5.13)

решение которого даст распределение 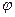, а следовательно, и скоростей по (5.12) и давлений (по (5.8)), т. е. полное реше­ние задачи гидродинамики.

Подстановка уравнений (5.10) в условие (5.11) дает урав­нение Лапласа:

. (5.14)

Без доказательства примем, что линии j=const и y=const взаимно перпендикулярны (функции j и y — орто­гональны), т. е. gradj 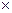grady 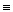0. Из теории функций комплексной переменной известно, что любая аналитическая

функция 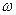удовлетворяет уравнению Лапласа и может быть представлена в виде

,

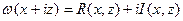где .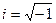

Функции R и I также удовлетворяют уравнению Лапла­са и, кроме того, ортогональны. Поэтому, если при решении задачи гидродинамики установлено, что j= R, то должно вы­полняться условие y= I, или, если j= I, то y = R.

Рассмотрим некоторые простейшие примеры:

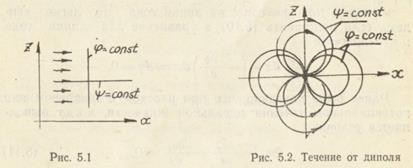
А) w(x+iz)=a(x+iz)=ax+iaz, где а = const.

Если j = ах, то 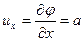; u_y =0 и y= az.

Уравнение линий постоянного потенциала скорости (j=const) — x =const (рис. 5.1).

Уравнение для линий тока (y=const) имеет вид z =const, т. е. рассмотренный случай — это случай течения жидкости вдоль оси х с постоянной во всем пространстве скоростью;

Б) .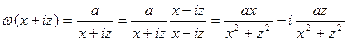

Если 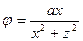, то .

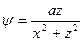Уравнение для линии тока (y = const) имеет вид

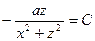или 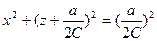- уравнение окружности (рис. 5.2).

Уравнение линии постоянного потенциала скорости

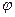( = const) также преобразуется к виду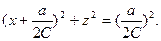

Полученное течение называется течением от диполя;

в)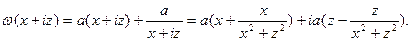

Если .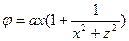

Уравнение линий тока 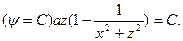В частном случае при С=0 уравнение линии тока имеет два решения:

z=0 и x ²+ z ²=1.

Поскольку на твердой поверхности при течении идеаль­ной жидкости нормальная составляющая скорости равна ну­лю, то уравнение контура твердого тела является также и уравнением для линии тока. Поэтому в рассмотренных при­мерах любая линия тока может быть взята в качестве кон­тура обтекаемой жидкостью поверхности тела.

Если в качестве контура твердого тела принять зависи­мость x ²+ z ²=1, то с внешней стороны от окружности полу­чим картину обтекания цилиндра потенциальным потоком (рис. 5.3), имеющим при х = - 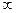скорость невозмущенного поток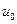а = а.

Решение задач по гидромеханике сводится обычно к на­хождению силы взаимодействия жидкости с обтекаемым телом. Наметим дальнейшие шаги в решении задачи обтека­ния цилиндра единичного радиуса. Зная уравнение для ,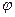

легко найт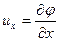и и 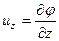. При нахождении распределе­ния скоростей по поверхности цилиндра удобно перейти к цилиндрическим координатам

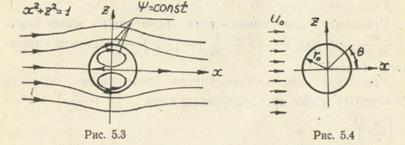
(x=r cosQ; z=r sinQ — рис. 5.4), тогда на поверхности цилиндра x =соsQ; z=sinQ; u_x1 = 2a sin²Q; u_z1= —2a sinQcosQ. Нетрудно вычислить

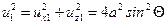(5.15)

Уравнение Бернулли в случае, когда плоскость хz горизонтальна, имеет вид

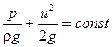
Приравняв удельные энергии невозмущенного потока с параметрами и₀, р₀ и жидкости на поверхности цилиндра, найдем

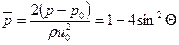(5.16)

На рис. 5.5 приведены теоретические и экспериментальные распределения давлений по поверхности цилиндра. Сила со­противления Р_х= 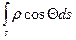с учетом (5.16), т.е. для идеальной жидкости, окажется равной нулю. Это решение полу­чило название парадокс Даламбера.

Дата добавления: 2015-05-23