Ламинарное течение в плоском клиновидном зазоре

Решение этой задачи иллюстрирует возникновение под­держивающей силы в подшипниках скольжения при наличии

смазывающего слоя жидкости.

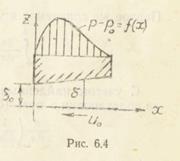
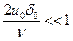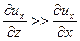Пусть нижняя пластина (рис. 6.4) движется со скоростью и₀ в направлении отрицательной оси х, а давление слева и справа от неподвижной пластины равно р₀. При малой величине зазора ₀ и высокой вязкости жидкости (т. е. при Re = ) в уравнении (3.10`) можно (см. 6.4) пренебречь инерционными членами и принять = 0. Кроме того, так как и Х = 0, то уравнение движения (3.10') в проекции на ось х можно записать в виде (6.9). В тонком слое величина не зависит от z. Проинтегрируем дважды уравнение (6.9) по z:

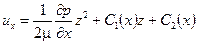
При граничных условиях и_х= — и₀ при z=0; и_х =0 при z= ,

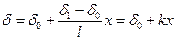(6.13)

k= 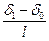—параметр клиновидного слоя ( 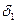—зазор при x=l),

получим

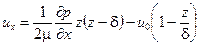(6.14)

Проинтегрируем уравнение неразрывности (при и_у=0) (2.13') по z.

Получим

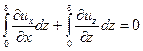, (6.15)

Поскольку 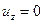при z=0 и при z= , то

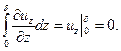
Первое же слагаемое в условиях данной задачи

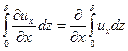
С учетом найденных соотношений уравнение (6.15) после подстановки в него (6.14) и интегрирования даст

,

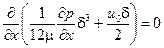т. е. выражение в скобках есть некоторая постоянная С'/2.

Тогда

(6.16)

Поскольку 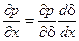, то с учетом (6.13)

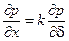
и уравнение (6.16) примет вид

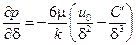(6.17)

Проинтегрируем (6.17) по : р=- .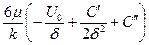

Постоянные интегрирования 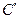и С" найдем из граничных условий: р = ро при х=0 и при х=1. После преобразований окончательно получим

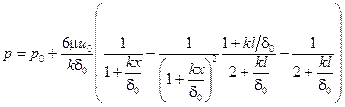(6.18)

Расчеты по этой зависимости показывают, что на всей длине l p>p 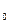- Эпюра избыточных давлений приведена на рис. 6.4. Уравнение (6.18) позволяет вычислить величину поддерживающей силы.

Дата добавления: 2015-05-23