Сопротивление гидравлически шероховатых труб при турбулентном режиме течения жидкости

Гидравлически шероховатые трубы характеризуются неравенством D > d или 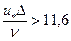, которое после преобразований можно представить в виде

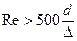(6.44)

При выводе уравнения для расчета lпредполагается, что в ядре потока справедливо уравнение (6.35), но постоянная интегрирования С находится из условия при z = D 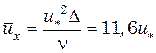(см. 6.30), т.е.

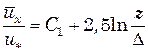
Вычислим среднюю скорость. Получим

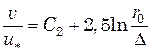
или с учетом (6.33) и (6.40)

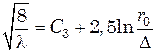
Это выражение после экспериментального уточнения коэффициента С₃ хорошо аппроксимируется более простым (формула Шифринсона):

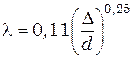6,45

которое применимо при выполнении условия (6.44). В области 20 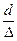<Rе<500 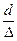на коэффициент 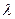оказывает влияние как число Re, так и относительная шероховатость 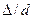. Обобщенная зависимость для расчета 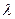справедливая как для гладких, так и для шероховатых труб, была получена А. Д. Альтшулем:

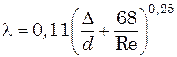6,46

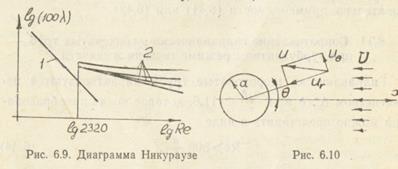
На рис. 6.9 приведена зависимость 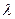от Re и 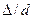в областях ламинарного (линия 1) и турбулентного (линия 2) режимов течения (диаграмма Никурадзе).

6.12. Ламинарное обтекание шара (задача Стокса) |

Течение со столь малыми скоростями, при которых в уравнении Навье-Стокса можно пренебречь инерционными слагаемыми по сравнению с трением, называется ползущим.

При ползущем движении шара относительно вязкой жидкости уравнения (3.10') примут вид (при F=0):

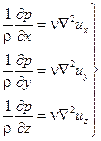6.47

Пусть центр покоящегося шара находится в начале координат, а при большом удалении от шара жидкость течет вдоль оси х (рис. 6.10). Тогда граничные условия следует записать так:

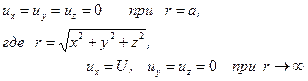
Для замыкания системы уравнений следует воспользоваться и уравнением неразрывности (2.13').

Задачу обтекания шара удобно решать в сферической системе координат. В силу симметрии задачи относительно оси х будем иметь

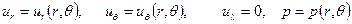
и уравнения (6.47) и (2.13') в сферической системе в этом случае примут вид

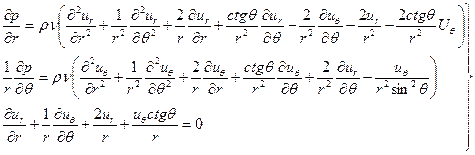6.48

Граничные условия:

при r=a ;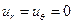

при r 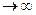u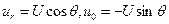

После интегрирования [2] найдем:

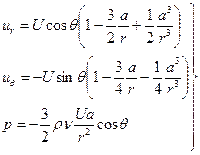6.49

На основе (3.5), записанных в сферических координатах, и с учетом (6.49) можно вычислить нормальную и касательную составляющие напряжения на поверхности шара: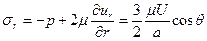

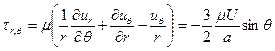
Величина равнодействующей силы (она направлена оче­видно вдоль оси х) может быть вычислена по формуле

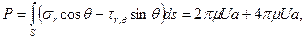
или

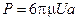6.50

Формула (6.50) называется «формулой Стокса». Она определяет силу сопротивления, возникающую при обтекании шара вязким потоком жидкости при ламинарном течении. Формула справедлива при условии (d=2a):

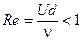
Рис. 6.11. Зависимость коэффициента сопротивления (при обтекании шара) от Re

Из решения видно, что 1/3 полной силы связана с силами давления, а 2/3 — с силами трения.

В прикладной гидромеханике для расчета силы сопротивления при обтекании тел любой формы принята формула

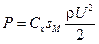6.51

где С_х — коэффициент сопротивления; s_m — площадь миделевого сечения, т. е. проекции тела на плоскость, перпендикулярную к направлению относительного движения тела и жидкости.

Приравняв (6.50) и (6.51), нетрудно найти, что при ламинарном обтекании шара (s_M=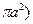

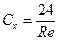
При переходе к турбулентному режиму обтекания влияние числа Re вырождается (рис. 6.11).

Формула (6.50) и (6.51) позволяет вычислить скорость осаждения твердых частиц в жидкости. Так, сила тяжести частицы диаметром d, плотность материала которой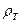

.

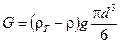При равномерном осаждении 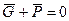Тогда с учетом (6.50) (при ламинарном осаждении) найдем

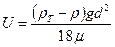
Дата добавления: 2015-05-23