Сила давления на плоскую поверхность тела

Равновесие жидкости в центробежном поле

На жидкостные частицы, находящиеся во вращающемся с постоянной скоростью вокруг вертикальной оси цилиндри­ческом стакане, действуют сила тяжести mg центробежная сила 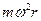(рис. 4.7). Следовательно, в этом случае

X=w²r cos(r, x); Y=w²r cos(r, y); Z=-g

Или

X=w²x; Y=w²y.

Подставим эти выражения в (4.3) и проинтегрируем по­следнее. Получим

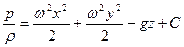(4.10)

или

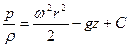(4.11)

При р = const уравнение (4.10) преобразуется в уравне­ние поверхности уровня-—уравнение параболоида вращения. Постоянную интегрирования С в (4.11) найдем из началь­ного условия р = р₀ при r = 0 и z=z₀..

Тогда

.

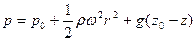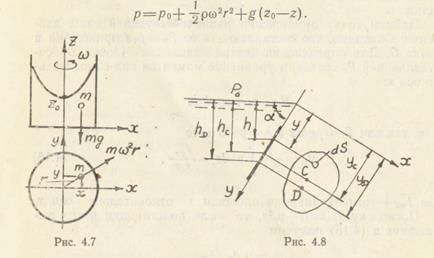
Силы давления, действующие на каждый элемент поверх­ности ds (рис. 4.8), параллельны, т.е. суммирование их мож­но проводить алгебраически:

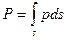(4.12)

и результирующая сила Р всегда направлена по внутренней нормали к плоской поверхности. Подставим (4.9) в (4.12). С учетом того, что h= ysina, получим

.

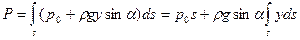Статический момент площади s относительно оси х мож­но записать в виде ,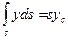

где точка С — центр тяжести площади s. Поскольку y_c sina= h_c, то

Р =Р₀+P (4.13)

где Po=p₀s,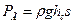

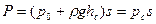, (4.14)

т. е. для вычисления величины равнодействующей силы дав­ления необходимо знать давление р_с в центре тяжести пло­щади.

Найдем точку приложения равнодействующей силы дав­ления. Очевидно, что составляющая ее P₀=p₀s приложена в точке С. Для определения центра давления (точки D) со­ставляющей Р_Г составим уравнение моментов сил относитель­но оси х:

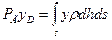
или, т.к. P_Г=rgh_cs и h=y sina, то

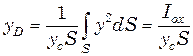, (4.15)

где I _ох — момент инерции площади s относительно оси х. Поскольку I_0X=I_C+ 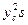, то после подстановки этого вы­ражения в (4.15) получим

,

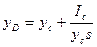где I_с — момент инерции площади относительно горизонталь­ной оси, проходящей через центр тяжести площади.

Дата добавления: 2015-05-23