Гидравлические потери на местных сопротивлениях

Гидравлические потери по длине

Уравнение Бернулли для сети с насосом

Если выполняется условие

то для обеспечения подачи жидкости от сечения 1 к 2необходимо сообщить ей энергию внешним источником, или насосом.

Удельная энергия, сообщаемая жидкости насосом, называется полезным напором и обозначается Н, м. Уравнение баланса энергий в этом случае имеет вид

(7.8)

Это уравнение позволяет для заданной схемы трубопроводов рассчитывать Н, а следовательно, подобрать насос. Поскольку слагаемые 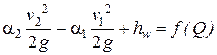, то уравне
ние (7.8) можно записать так:

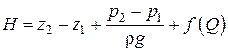(7.9)

Эта зависимость называется характеристикой сети

Составим уравнение Бернулли (7.7) для горизонтального участка трубы (см. рис. 6.8). В этом случае 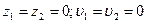. Из (7.7) получим или с учетом (6.12)

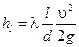(7.10)

Уравнение (7.10) можно получить из (7.2) с учетом (3.19) и (6.26).

Для расчета их используется формула

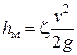(7.11)

где z — коэффициент местного сопротивления, обычно определяемый опытным путем.

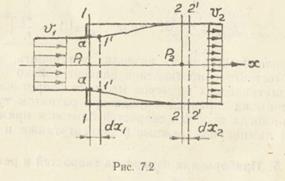
Гидравлические потери при внезапном расширении (рис. 7.2) можно найти аналитически. Рассмотрим решение этой задачи подробно ( вгидравлике она получила название «Теорема Борда»).

К жидкости, находящейся в момент t в объеме между сечений 1 — 1 и 2 — 2, применим теорему об изменении количества движения (3.2). В проекции на ось х

(7.12)

где

(7.13)

За время dt жидкость сместится (сечение 1-1 в 1—а—1'—1'—а—1, сечение 2—2 в 2'—2') и займет объем 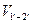. Изменение количества движения составит

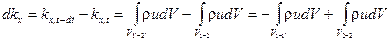(7.14)

Предположив, что в выбранных сечениях эпюра скоростей прямоугольная, и получим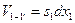

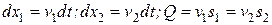. С учетом того, что , уравнение (7.14) можно привести к виду

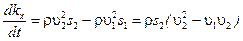(7.15)

Подставим (7.15) и (7.13) в (7.12), найдем

(7.16)

Для нахождения гидравлических потерь применим уравнение Бернулли (7.7) для сечений 1 и 2. Поскольку 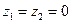, то

(7.17)

В условиях, когда в сечении u= 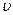; =1 с учетом (7.16), получим уравнение Борда для расчета гидравлических потерь при внезапном расширении потока:

(7.18)

С учетом соотношения 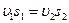представим (7.18) в виде (7.11):

, где

или

, где

Выполненный анализ позволил установить, что коэффициент местного сопротивления зависит только от соотношения геометрических размеров местного сопротивления. Однако этот вывод справедлив лишь при развитом турбулентном течении, когда профиль скоростей близок к прямоугольному.

При ламинарном режиме 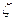зависит также и от Re.

Дата добавления: 2015-05-23