Приборы для измерения скоростей и расходов

Здесь мы рассмотрим только те приборы, принцип действия которых может быть объяснен с помощью уравнения Бернулли:

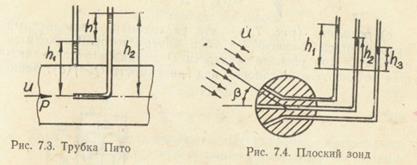
а) трубка Пито (рис. 7.3). В пьезометрической трубке 1, или трубке статического напора, уровень жидкости 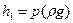. При обтекании устья трубки полного напора 2 происходит торможение потока, т. е. преобразование кинетической энергии в энергию давления, и h₂=p( 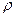g)+u²/(2g). Перепад уровней 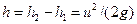т. е. прибор позволяет измерить локальную скорость в канале:

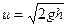
б) плоский зонд (рис. 7.4) применяется для измерения величины и направления локальной скорости в плоском потоке. Измерив перепады уровней h₂ — h 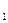и h₂ — h 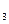, каждый из которых зависит от значения скорости u и угла b набегания
потока, получаем возможность нахождения и и b;

в) шаровой зонд — это шарик, в теле которого выполнено пять каналов: три — как показано на рис. 7.4, у плоского зонда и еще два - смещенных относительно канала 2 в горизонтальной плоскости. Применяется для измерения направления и величины локальной скорости в пространственном потоке;

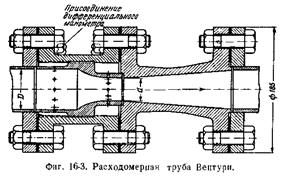
г) расходомер с соплом Вентури. Применим уравнение Бернулли (7.7) к сечениям 7 и 2 (рис. 7.5). В данном случае , 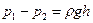. Подставив эти выражения и уравнение (2.6) в (7.1) и решив его относительно 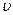, найдем

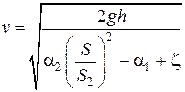
где s и s₂ – площади сечений трубы и горловины расходомера Вентури.

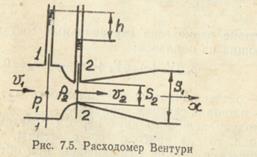
Расход жидкости вычислим по формуле Q= 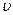s;

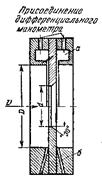
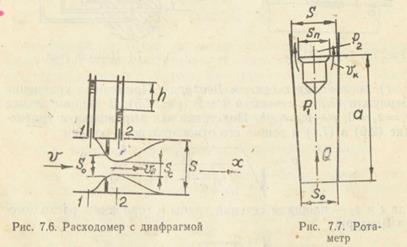
д) расходомер с диафрагмой (рис. 7.6). Установка тонкостенной шайбы вызывает сжатие потока, причем в сечении 2 площадь сечения струи s_c<s₀ (s₀ — площадь сечения отверстия). Их отношение s_c/s₀= 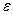называется коэффициентом сжатия струи. По аналогии с предыдущей задачей найдем

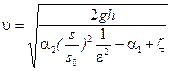
е) ротаметр (рис. 7.7) — это расходомер, выполненный из стеклянной конической трубки, внутри которой находится поплавок. При расходе жидкости Q поплавок устанавливается по высоте а. Установим вид зависимости Q=f(a). Запишем условие равновесия вертикальных

составляющих сил, действующих на поплавок:

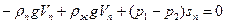
где Vn — объем поплавка; 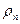— плотность материала поплавка; s_n —• площадь сечения поплавка.

Поскольку величины двух первых слагаемых не зависят от расхода, то для прибора р 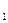—p₂ = const. Следовательно, гидравлические потери, возникающие при обтекании поплавка,

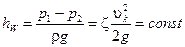
и скорость жидкости 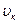в кольцевом канале ;

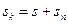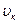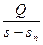= =const. Если выполнено условие s=s₀+ka(k — коэффициент пропорциональности), то получим Q= 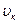(s₀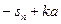

Дата добавления: 2015-05-23