Практична РОБОТА №2

Приклади обчислень елементарних функцій з використанням рядів Тейлора. Визначення похибок обчислень

2.1 МЕТА РОБОТИ

1 Вивчення основних визначень і положень теорії апроксимації функції.

2 Вивчення основних методів неперервної апроксимації функцій багаточленами Тейлора.

3 Апроксимація на ЕОМ за допомогою рядів Тейлора елементарних функцій.

2.2 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

Апроксимація

Нехай є функція f(x), вид якої дуже складний і для її обчислення потрібно багато часу або функція задана в деяких точках таблицею своїх значень

. (2.1)

Як правило необхідно знати значення величини y практично при будь-яких значеннях аргументу x і цих значень потрібно багато. Як це реально зробити? Для розв'язку такої проблеми служить задача апроксимації функцій, у якій дану функцію f(x) приблизно заміняють (апроксимують) деякою функцією, так, щоб відхилення j(x) від f(x) у заданому інтервалі [a,b] було мінімально можливим. Функцію f(x) називають апроксимованою, а функцію j(x) апроксимуючою.

При наближенні на неперервній множині точок відрізка [a,b] апроксимацію називають неперервною (або інтегральною). Якщо наближення будується на заданій дискретній безлічі точок {x_i} i=0,1,... відрізка [a,b], то апроксимацію називають точковою.

Рівномірне і середньоквадратичне наближення

Якщо наближення будується таким чином, що величина відхилення (модуль різниці двох цих функцій) задовольняє умові

(2.2)

то таке наближення (2.2) є рівномірним наближенням.

Часто використовується середньоквадратичне наближення функції f(x) функцією j(x). Тут намагаються одержати мінімальну величину середньоквадратичного значення модуля різниці апроксимованої та апроксимуючої функцій на усьому відрізку [a,b]:

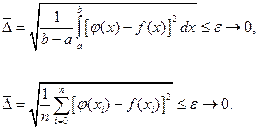(2.3)

Перша формула використовується при неперервній апроксимації, а друга при дискретній апроксимації.

Апроксимація багаточленами (поліномами)

Найчастіше для апроксимації використовуються алгебраїчні багаточлени (поліноми) наступного виду

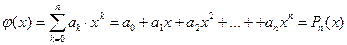. (2.4)

Максимальне значення степеня змінної x (значення величини n) називається порядком апроксимуючого багаточлена або порядком полінома.

Використання рядів для рівномірної апроксимації

Можливість побудови багаточлена, що рівномірно наближає дану функцію, випливає з теореми Вейєрштрасса про апроксимації. Зокрема, якщо f (x) на відрізку [a,b] розкладається у рівномірно збіжний ряд, то за апроксимуючий багаточлен можна взяти часткову суму ряду Тейлора і т.ін.

Розглянемо такі трансцендентні функції, що є сумами своїх рядів Тейлора:

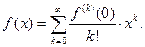(2.5)

Використавши перші члени ряду Тейлора, одержимо наближену формулу:

(2.6)

де,

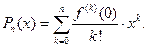(2.7)

Похибка

Залишок ряду 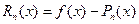є похибкою при заміні f(x) багаточленом P_n(x), тобто визначає абсолютну похибку обчислення f(x) із використанням формули (2.6). Для ряду (2.5) абсолютна похибка буде не більшою за абсолютною величиною залишкового члена ряду Тейлора у формі Лагранжа:

(2.8)

де x деяка невідома точка на відрізку [0,x].

Розкладання елементарних функцій у ряд Тейлора:

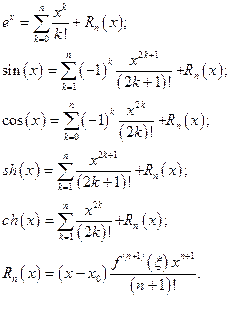
(2.9)

де x - точка на відрізку [0,x].

2.3 ЗАВДАННЯ

1 Обчислити за допомогою полінома n-ого степеня P_n(x), що рівномірно наближає на відрізку [a,b] функцію f(x), із таблиці завдань.

2 На ЕОМ набрати і налагодити програму.

4 Провести обчислення полінома P_n(x).

5 Оцінити відносну похибку обчислення P_n(x).

6 Провести розрахунки за допомогою програми MATLAB і порівняти результати.

2.4 КОНТРОЛЬНІ ПИТАННЯ

1 Визначення рівномірного наближення.

2 Визначення квадратичного наближення.

3 Поняття неперервної і точкової апроксимації.

4 Визначення багаточлена найкращого рівномірного наближення.

5 Використання залишкового числа у формі Лагранжа для оцінки похибки.

2.5 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

№	Апроксимована функція f(x)	Степінь апроксимуючого полінома (n)	x1	x2
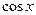
			62°	88°
			0.15(рад)	0.56(рад)
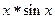
			0.01(рад)	0.83(рад)
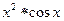
			0.32(рад)	0.53(рад)
			55°	97°
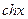
			40°	93°
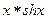
			0.25(рад)	1.27(рад)
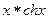
			0.63(рад)	1.65(рад)
			0.78(рад)	1.80(рад)
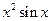
			0.91(рад)	1.94(рад)
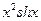
			0.35(рад)	1.37(рад)
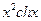
			0.43(рад)	1.45(рад)
			12°	94°
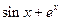
			57°	159°
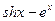
			73°	175°

Дата добавления: 2015-05-23