Практична РОБОТА №1

Визначення похибок при комп’ютерному моделюванні

1.1 МЕТА РОБОТИ

1 Вивчення джерел і класифікація похибок, що виникають при розв'язку на ЕОМ наукових та інженерних задач.

2 Вивчення правил наближених обчислень і оцінка похибок.

3 Оцінка з використанням ЕОМ абсолютної і відносної похибок функцій багатьох змінних.

1.2 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

Одержуваний за допомогою ЕОМ результат y майже завжди, за рідкісним винятком, містить похибку, тобто є наближеним.

Основні джерела і класифікація похибок математичного моделювання:

а) математична модель є наближеним описом реальної наукової, інженерної або іншої практичної задачі;

б) вихідні дані містять похибки, внаслідок того, що вони отримані в результаті вимірювань або інших розрахунків;

в) математичні методи у більшості випадків є наближеними;

г) через обмеженість розрядності обчислювальної машини і використовуваних способів представлення чисел в ЕОМ при введенні і виведенні, а також при виконанні арифметичних операцій здійснюється заокруглення.

Величина похибки d_н – що виникає внаслідок перших двох причин називається неусувною похибкою. Похибка d_м джерелом якої є метод називається похибкою методу. Обчислювальною похибкою називається похибка d_у, що виникає при введенні, виводі і виконанні арифметичних операцій на ЕОМ.

Максимальна відносна похибка заокруглення називається машинним епсилон e_m і визначається розрядністю ЕОМ.

Абсолютна і відносна похибки

Нехай a - точне значення деякої величини, а ^* - відоме наближене значення цієї величини. Додатна величина 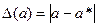називається абсолютною похибкою величини a. Відношення абсолютної похибки величини а до її абсолютного значення називається відносною похибкою.

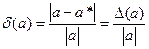. (1.1)

Максимальне значення D(а) називається граничною абсолютною похибкою і позначається `D(а). Відповідно гранична відносна похибка дорівнює:

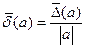. (1.2)

Іноді слово “ гранична” не зазначають і під абсолютною і відносною мають на увазі абсолютну і відносну граничні похибки. Нижче слово “граничне“ також не буде повторюватися.

Похибки арифметичних операцій

а) при додаванні і відніманні двох величин їхні абсолютні похибки додаються:

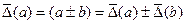. (1.3)

б) при множенні і діленні двох величин їхні відносні похибки визначаються:

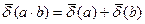, (1.4)

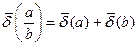. (1.5)

в) при піднесені у степінь наближеної величини її відносна похибка збільшується на показник степеня:

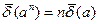. (1.6)

Похибка функцій

Нехай а - наближене значення аргументу x функції y=f(x), а D а - абсолютна похибка, тобто 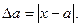При Dа<<1 для оцінки абсолютної похибки і відносної похибок використовуються наступні вирази:

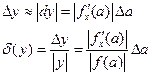. (1.7)

Аналогічні співвідношення можна записати для функції декількох змінних, наприклад, якщо U=f(x,y,z), то при:

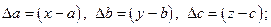
маємо:

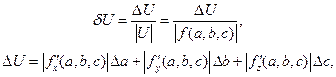(1.8)

де 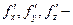частинні похідні за відповідними аргументами.

Визначення машинного епсилон

При виконанні операції додаванні двох чисел 1+e при e<<1 внаслідок заокруглення буде отримане результуюче число 1. Оскільки точне значення суми повинно дорівнювати 1+e, а одержуване значення дорівнює 1, то абсолютна похибка суми D(1+e) дорівнює e. Так як за означенням машинне епсилон e_m є відносною похибкою округлення, то маємо

.

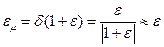Таким чином, якщо визначити таке значення e при якому 1+e = 1, то це значення буде дорівнює e_m.

З цією метою в циклі досить організувати обчислення послідовності: e_n+1=e_n/2, n=0,1,..., починаючи з e₀=1 і перевірку виконання умови 1+e_n+1=1. При деякому n умова 1+e_n+1=1 буде виконана, звідси і визначається значення e_m=e_n+1.

1.3 ЗАВДАННЯ

1 Розробити текст програми для обчислення машинного епсилон.

2 Провести теоретичне виведення формули для оцінки абсолютної і відносної похибок функції U(x,y,z):

3 Вид функцій f(x,y), j(x,z) зазначений у таблиці індивідуальних завдань.

4 Розробити текст програми для обчислення абсолютної і відносної похибки функції U(x,y,z).

5 На ЕОМ набрати і налагодити програму.

6 Провести розрахунок абсолютної і відносної похибки функції U(x,y,z), для зазначених у таблиці значень аргументів, прийнявши, що ці вхідні дані мають відносну похибка 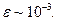Результати занести в таблицю.

7 Для виконання пункту 5 використати програму MATLAB і порівняти результати.

1.4 КОНТРОЛЬНІ ПИТАННЯ

1 Що таке математичне моделювання?

2 Основні етапи математичного моделювання.

3 Основні джерела похибки математичного моделювання.

4 Класифікація похибок.

5 Що таке заокруглення числа?

6 Визначення абсолютної і відносної похибок.

7 Правила оцінки абсолютних і відносних похибок арифметичних операцій.

8 Похибки функцій.

9 Як кількість вірних знаків пов'язана з похибкою числа?

10 Що таке машинне “ епсилон “?

1.5 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

№	f(x,y)	j(x,z)	x	y	z
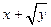
		sin(x+z)	2.01	1.1	0.5
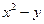
		cos(x+z)	1.3	0.34	0.23
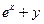
		ln(x+z)	1.5	2.4	8.5
	x+y	x-z	0.4	0.71	0.55
	x/y	z^3+x^2	7.6	4.3	3.5
	6x^3-siny	e^x-z	1.5	1.8	4.3
	cos(x-y)	sin(x+z)	0.43	0.21	4.3
	x^4+y	ln(x-z)	3.2	5.5	4.8
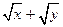
		e^x+z	2.1	2.3	1.2
	e^x+z	x/z	0.	5.2	6.8
	5x^3	6y^3+sinz	0.3	0.5	1.4
	sin(x-y)	x+z	5.8	4.2	8.5
	ln(x-y)	x	1.5	7.5	9.8
	sin(x+z)		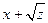2.4	0.3	1.9
	e^x+7y	5x+z^2	0.35	10.4	30.5

Дата добавления: 2015-05-23