Симплексний метод

Симплексний метод є універсальним, оскільки дозволяє розв’язати практично будь-яку задачу лінійного програмування, яка записана у канонічному вигляді.

Ідея симплекс-методу або методу послідовного покращення плану полягає у тому, що починаючи з деякого початкового опорного рішення здійснюється послідовно спрямоване переміщення по опорним рішенням задачі до оптимального. Значення цільової функції при цьому переміщенні для задач на максимум не спадає. Оскільки число опорних рішень є скінченим, то через скінчене число кроків одержують оптимальний опорний розв’язок.

Опорним розв’язком називають базисний невід’ємний розв’язок.

Алгоритм симплексного методу

1. Математична модель задачі повинна бути канонічною.

2. Відшукується вихідний опорний розв’язок і здійснюється перевірка його на оптимальність. Для цього заповнюється симплексна таблиця. Всі рядки таблиці першого кроку за виключенням рядка (індексний рядок) заповнюються за даними системи обмежень та цільової функції.

БЗ – базисна змінна.

Індексний рядок для змінних визначається за формулою

, ,

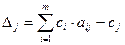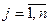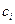
	БЗ			...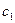
		...
				...
				...
...	...	...	...	...	...	...
				...
			...

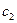
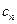
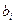
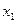
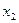
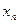
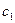
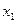
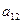
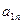
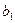
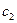
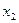
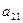
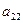
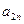
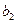
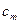
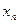
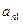
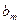
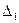
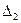
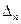
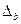
для вільного члена за формулою

.

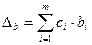Можливі наступні випадки при розв’язанні задачі на максимум:

- якщо всі оцінки 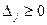, то знайдений розв’язок є оптимальним;

- якщо хоча б одна оцінка , але при відповідній змінній немає жодного додатного коефіцієнта, розв’язання задачі припиняється, тому що 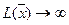, тобто цільова функція є необмеженою у області припустимих розв’язків;

- якщо хоча б одна оцінка від’ємна, а при відповідній змінній є хоча б один додатній коефіцієнт, то необхідно переходити до другого опорного розв’язку;

- якщо від’ємних оцінок в індексному рядку декілька, то у стовпець базисної змінної (БЗ) вводять ту змінну, якій відповідає найбільша за абсолютною величиною від’ємна оцінка.

Якщо хоча б одна оцінка 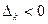, то -й стовпець приймається за ключовий. За ключовий рядок приймається такий, якому відповідає мінімальне відношення вільних членів 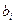до додатних елементів -го стовпця. Елемент, який знаходиться на перетині ключових рядка і стовпця називається ключовим елементом.

3. Заповнюється симплексна таблиця другого кроку:

- переписується ключовий рядок, з діленням кожного його елемента на ключовий елемент;

- заповнюється базисний стовпець, при цьому всі елементи окрім ключового дорівнюють нулю;

- решта коефіцієнтів таблиці знаходяться за правилом прямокутника.

Наприклад, якщо 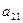є ключовим елементом, тоді у симплексній таблиці другого кроку

.

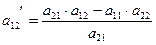Альтернативний оптимум

При розв’язанні задач лінійного програмування симплексним методом за критерій оптимальності приймають умову: оцінка вільних змінних 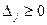для задач на максимум і умова 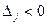для задач на мінімум.

Якщо на будь-якому кроці хоча б одна з оцінок вільної змінної 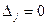, а решта 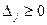для задач на максимум ( 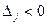для задач на мінімум), то прийнявши за ключовий стовпець той стовпець, де 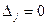та знайдемо новий оптимальний розв’язок, при якому значення цільової функції не змінюється. У цьому випадку задача має альтернативний оптимум.

Критерієм альтернативного оптимуму при розв’язанні задач симплексним методом є рівність нулю хоча б однієї оцінки вільної змінної .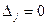

Якщо тільки одна оцінка вільної змінної дорівнює нулю, тоді розв’язок задачі знаходиться за формулою

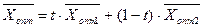, де .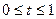

Якщо дві оцінки і більше, наприклад 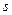, вільних змінних дорівнюють нулю, тоді оптимальний розв’язок знаходиться за формулою

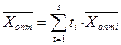, де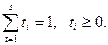

Дата добавления: 2015-05-23