Графічний розв’язок систем т лінійних нерівностей з двома змінними

Дано систему т лінійних нерівностей з двома змінними

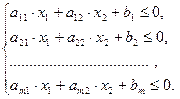(3.1)

Знак деяких або всіх нерівностей може бути „ ”.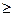

Розглянемо першу нерівність системи (3.1) у системі координат . Побудуємо пряму , яка є граничною прямою. Ця пряма ділить площину на дві півплощини (1) і (2).

Напівплощина (1) вміщує початок координат. Для визначення, з якого боку від граничної прямої розміщена задана напівплощина необхідно взяти довільну точку на площині (краще початок координат) і підставити координати цієї точки у нерівність. Якщо нерівність справедлива, то напівплощина звернена у бік цієї точки, якщо не справедлива – то у протилежний бік від точки. Напрямок напівплощини на малюнку позначається стрілкою.

Розв’язком кожної нерівності системи є напівплощина, яка вміщує граничну пряму і розміщена по одну сторону від неї.

Перетином напівплощин, кожна з яких визначається відповідною нерівністю системи, називається областю розв’язків системи (ОР).

Область розв’язків системи, яка задовольняє умовам невід’ємності (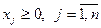), називається областю невід’ємних або припустимих розв’язків (ОПР).

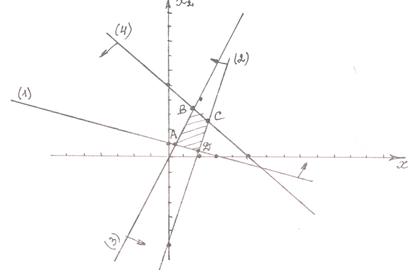
Приклад. Знайти ОР і ОПР системи нерівностей і визначити координати кутових точок ОПР.

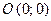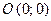Знайдемо ОР системи. Для цього побудуємо граничну пряму і підставимо координати точки у нерівність (1): Координати точки не задовольняють нерівності (1), тому розв’язком цієї нерівності є напівплощина, що не вміщує точки .

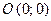(1) 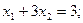При При

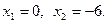(2) При При

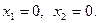(3) При При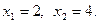

(4) При При

Областю розв’язків і областю припустимих розв’язків є чотирьохкутник 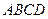. Знайдемо кутові точки чотирьохкутника.

.

; .

.

.

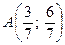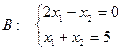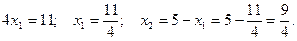
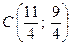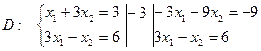
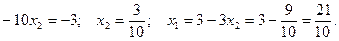
Дата добавления: 2015-05-23