Графічний метод. Найбільш простим і наочним методом лінійного програмування є графічний метод

Найбільш простим і наочним методом лінійного програмування є графічний метод. Він застосовується для розв’язання задач лінійного програмування, які задано у неканонічній формі і багатьма змінними у канонічній формі при умові, що вони вміщують не більше двох вільних змінних.

З геометричної точки зору у задачах лінійного програмування відшукується така кутова точка або набір точок із припустимої множини розв’язків, на якій досягається сама верхня (нижня) лінія рівня, розміщена далі (ближче) інших у напрямку найбільш швидкого зростання.

Для знаходження екстремального значення цільової функції при графічному розв’язанні задач лінійного програмування використовують вектор 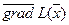на площині .

З курсу вищої математики відомо, що для функції двох змінних , що є диференційованою у точці , градієнтом функції називається вектор, координатами якого є значення частинних похідних у точці .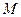

Градієнт функції характеризує напрямок і величину максимальної швидкості зростання цієї функції у точці.

Для визначення геометричного змісту градієнта функції введемо поняття поверхні рівня.

Поверхнею рівня функції 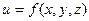називається поверхня, на якій ця функція зберігає постійне значення.

Градієнт функції у даній точці ортогональний до цієї поверхні.

У випадку функції двох змінних, замість поверхні рівня будуть фігурувати лінії рівня.

Надалі будемо позначати градієнт цільової функції 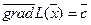. Цей вектор показує напрямок найшвидшої зміни цільової функції.

,

де - одиничні вектори за осями 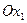та відповідно.

Таким чином . Координатами вектора 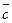є коефіцієнти цільової функції .

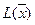Алгоритм розв’язання задачі

1. Знаходимо область припустимих розв’язків системи обмежень задачі.

2. Будуємо вектор .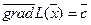

3. Проведемо лінію рівня , яка ортогональна до вектора .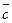

4. Лінію рівня переміщуємо за напрямком вектора 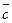для задач на максимум і в напрямку протилежному 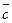- для задач на мінімум.

Переміщення лінії рівня здійснюється до тих пір, доки у неї не буде тільки однієї спільної точки з областю припустимих розв’язків. Ця точка визначає єдиний розв’язок задачі лінійного програмування і буде точкою екстремуму. Якщо ж лінія рівня буде паралельною одній з сторін області припустимих розв’язків, то у цьому випадку екстремум розглядається у всіх точках відповідної сторони, а задача лінійного програмування буде мати нескінчену множину рішень. У цьому випадку говорять, що така задача має альтернативний оптимум і її розв’язок знаходиться за формулою

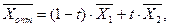
де 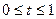, а 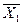, - оптимальні рішення у кутових точках області припустимих розв’язків.

Задача лінійного програмування може бути нерозв’язаною, коли обмеження, що її визначають, будуть суперечними.

5. Знайдемо координати точки екстремуму і значення цільової функції в ній.

Дата добавления: 2015-05-23