Цілочислове програмування

Транспортна задача

Транспортна задача – одна з розповсюджених задач лінійного програмування. Її мета – розробка найбільш раціональних шляхів і способів транспортування товарів, усунення найбільш віддалених, зустрічних, повторних перевезень. Все це скорочує час просування товарів, зменшує витрати підприємств, пов’язаних із здійсненням процесів забезпечення сировиною, матеріалами, паливом, обладнанням тощо.

У загальному вигляді задачу можна представити наступним чином: у т пунктах виробництва 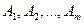маємо однорідний вантаж відповідно у кількості 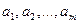. Цей вантаж необхідно доставити у п пунктів призначення відповідно у кількості 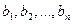. Вартість перевезення одиниці вантажу (тариф) із пункту до пункту дорівнює .

Необхідно скласти план перевезень, яких дозволяє перевезти весь вантаж при мінімальних транспортних витратах.

У залежності від співвідношення між сумарними запасами вантажу і сумарними потребами у них, транспортні задачі можуть бути закритими і відкритими.

Якщо , тоді транспортна задача називається закритою.

Якщо , тоді транспортна задача називається відкритою.

Позначимо через 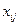кількість вантажу, який перевозять з пункту до пункту .

Відкрита транспортна задача

Умову даної задачі запишемо у вигляді розподільчої таблиці.

Математична модель закритої транспортної задачі має наступний вид

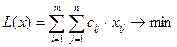
при обмеженнях

			...		...
		...		...
				...		...
				...		...
...	...	...	...	...	...	...	...
				...		...
...	...	...	...	...	...	...	...
				...		...

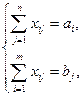
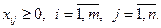
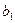
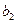
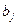
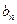
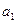
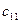
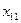
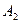
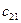
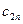
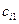
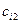
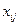
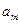
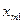
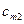
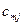
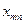
Оптимальним розв’язком задачі є матриця 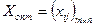, яка задовольняє системі обмежень і дозволяє мінімізувати цільову функцію.

Транспортна задача, яка є задачею лінійного програмування, може бути розв’язана симплексним методом, але наявність великої кількості змінних і обмежень робить обчислення громіздкими. Тому для розв’язання транспортних задач розроблено спеціальний метод, який має ті ж самі етапи, що і симплексний метод, а саме:

- знаходження вихідного опорного розв’язку;

- перевірка цього розв’язку на оптимальність;

- перехід від одного опорного розв’язку до іншого.

Знаходження вихідного опорного розв’язку

У розподільчій таблиці клітини, у яких помістимо вантажі, називаються зайнятими і їм відповідають базисні змінні опорного розв’язку. Інші клітини називаються незайнятими або пустими і їм відповідають вільні клітини. У верхньому правому куті кожної клітини будемо записувати тарифи. Існують декілька способів знаходження вихідного опорного розв’язку.

Розглянемо метод мінімального тарифу. Згідно з цим методом, вантажі розподіляються у першу чергу в ті клітини, в яких знаходиться мінімальний тариф перевезень . У подальшому поставки розподіляються у незайнятих клітинах з найменшими тарифами з урахуванням запасів, що залишилися у постачальників, і задоволення попиту споживачів. Процес розподілу продовжують до тих пір, доки всі вантажі від постачальників не будуть вивезеними, а споживачі не будуть задоволеними. При розподілі вантажів може бути, що кількість зайнятих клітин менше, ніж . У цьому випадку недостатня їх кількість заповнюється клітинами з нульовими поставками, такі клітини називаються умовно зайнятими.

Нульові поставки розміщують у незайняті клітини з урахуванням найменшого тарифу таким чином, щоб у кожному рядку і стовпці було не менше, ніж по одній зайнятій клітині.

Покращення отриманого опорного плану методом потенціалів

Після завершення першого етапу розв’язку задачі знайдені невідомі можна розбити на дві групи – базисні (зайняті) і вільні.

Представимо цільову функцію наступним чином

,

де 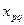- вільні змінні; - знайдений опорний план, а значення отримаємо за допомогою методів потенціалів.

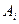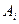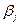Поставимо у відповідність кожному з пунктів відправлення вантажів деяку величину - „потенціал” пункту . Аналогічно кожному пункту призначення величину - „потенціалу” пункту .

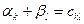Для кожного базисного невідомого складаємо рівняння , де - вартість перевезення з пункту до пункту 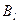. Розв’язуємо систему рівнянь і знаходимо всі потенціали та .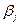

Тепер для кожної вільної змінної 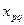обчислюємо суму - посередні вартості та заносимо до таблиці.

Наступним кроком є визначення різниць між справжніми вартостями перевезень та посередніми вартостями, які відповідають вільним клітинам.

Якщо всі величини невід’ємні, то початковий знайдений розв’язок є оптимальним. Якщо , тоді необхідно перейти до іншого базису.

Альтернативний оптимум у транспортних задачах

Ознакою наявності альтернативного оптимуму у транспортних задачах є рівність нулю хоча б однієї з оцінок вільних змінних у оптимальному розв’язку 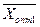. Зробивши перерозподіл вантажів відносно клітини, що має , одержимо новий оптимальний розв’язок 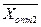, при цьому значення цільової функції (транспортних витрат) не зміниться.

Якщо одна різниця дорівнює нулю, тоді оптимальний розв’язок знаходиться за формулою

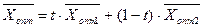, де .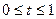

Виродженість у транспортних задачах

При розв’язанні транспортної задачі може бути, що кількість зайнятих клітин менша за . У цьому випадку транспортна задача може мати вироджений розв’язок. Для можливого його виключення, доцільно поміняти місцями постачальників і споживачів або ввести у вільну клітину з найменшим тарифом нульову поставку. Нуль вміщують у таку клітину, щоб у кожному рядку і кожному стовпці було не менше однієї зайнятої клітини.

Відкрита транспортна задача

При відкритій транспортній задачі сума запасів не співпадає з сумою потреб, тобто .

При цьому:

а). Якщо 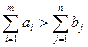, тоді обсяг запасів перевищує обсяг споживання, всі споживачі будуть задоволені повністю і частина запасів залишається не вивезеною. Для розв’язання такої задачі вводять фіктивного ( 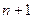-го) споживача, потреби якого .

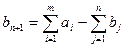Модель такої задачі набуває вигляду

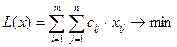
при обмеженнях

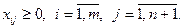
б). Якщо , тоді обсяги споживання перевищують обсяги запасів і частина споживачів залишається незадоволеною. Для розв’язання такої задачі вводять фіктивного (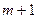 -го) постачальника, обсяги поставок якого .

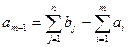Модель такої задачі набуває вигляду

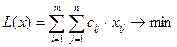
при обмеженнях

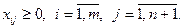
При введенні фіктивного постачальника або споживача, задача стає закритою і розв’язується за раніше розглянутим алгоритмом, причому тарифи, що відповідають фіктивному постачальнику або споживачу більше або дорівнюють найбільшому з усіх тарифів. У цільовій функції фіктивний постачальник або споживач не враховується.

Дата добавления: 2015-05-23