Види математичних моделей

Математична модель задачі лінійного програмування може бути представлена у канонічній і неканонічній формі.

Якщо всі обмеження системи задано рівняннями і змінні 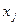є невід’ємними, тоді таку модель називають канонічною. Якщо хоча б одне обмеження є нерівністю, тоді модель задачі лінійного програмування називають неканонічною.

Для переходу від неканонічної до канонічної моделі необхідно у кожну нерівність ввести балансову змінну . Якщо знак нерівності „ ”, тоді балансова змінна вводиться із знаком „+”, якщо знак нерівності „ 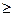” - із знаком „-”. У цільову функцію цільові змінні не вводяться.

Таким чином, щоб скласти математичну модель задачі лінійного програмування необхідно:

- ввести позначення змінних;

- виходячи з мети економічних досліджень, скласти цільову функцію;

- враховуючи обмеження у використанні економічних показників задачі та їх кількісні закономірності, записати систему обмежень.

Приклад. Скласти задачу про використання ресурсів.

Нехай на випуск п видів продукції 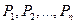витрачається т видів ресурсів (сировина, матеріали, праця, тощо) 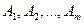. Відомі витрати ресурсів і -го виду на одиницю продукції -го виду, обсяг 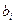ресурсів і -го виду і прибуток від реалізації одиниці продукції -го виду. Необхідно так організувати випуск продукції, виходячи із наявних ресурсів, щоб одержати найбільший прибуток.

Представимо вихідні дані задачі у вигляді таблиці

Таблиця

Вид ресурсу	Вид продукції	Запаси ресурсів, грн.
		...		...
			...		...
			...		...
...	...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...	...
			...		...
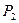
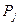
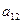
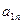
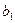
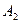
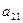
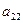
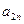
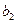
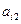
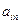
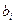
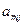
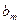
Прибуток від реалізації одиниці продукції			...		...
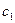
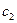
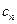
Випуск продукції			...		...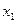

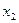
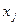
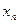
За шукані невідомі візьмемо - кількість одиниць випущеної продукції видів .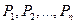

Складемо цільову функцію економіко-математичної моделі. Прибуток від випуску всієї продукції становить

Невідомі повинні задовольняти нерівностям, які показують, що фактичні витрати відповідного виду ресурсів не повинні перевищувати його наявний обсяг

Виходячи з економічного змісту задачі, невідомі можуть набувати тільки невід’ємних значень, тобто

Дата добавления: 2015-05-23