Імовірність події

Події (явища), які ми спостерігаємо можна розділити на три види. Подія, яка в певних умовах обов’язково відбувається називається достеменною подією. Подія, яка в певних умовах не може відбутися називається неможливою подією. Подія, яка в певних умовах може відбутись або не відбутись називається випадковою подією. Кожне повторення дослідження в цих умовах називають випробуванням. Прикладом достеменної події є падіння підкинутого вгору тіла в умовах земного тяжіння. Неможливою подією є, наприклад, випадання семи очок при киданні грального кубика, на гранях якого нанесені від однієї до шести точок. Прикладами випадкових подій є виграш у лотереї, випадання чотирьох очок на гральному кубику, народження у сім’ї дитини певної статі. Події будемо позначати великими буквами латинського алфавіту (або буквами з індексами), наприклад, А, В, С ₁, С ₂, D ₅. Достеменну подію позначатимемо буквою І, а неможливу — буквою О.

Теорія ймовірностей не може передбачити чи здійсниться окрема випадкова подія чи ні. Інакше складається ситуація, якщо випадкова подія може багато раз спостерігатися при виконанні одних і тих же умов. Виявляється, що більшість однорідних випадкових подій незалежно від їх природи підпорядковується певним закономірностям, які називають імовірнісними. Вивчення імовірнісних закономірностей масових однорідних випадкових подій є предметом теорії ймовірностей.

Будь-яка подія розглядається як результат випробування. Події називають несумісними, якщо здійснення однієї з них виключає здійснення інших подій у тому ж випробуванні. Декілька подій утворюють повну систему (групу), якщо підчас випробування достеменною подією є здійснення хоча б однієї з них. Події називають рівноможливими, якщо здійснення будь-якої з них не має жодних переваг перед здійсненням іншої. Кожен з можливих результатів випробування називатимемо елементарним виходом. Очевидно, всі елементарні виходи утворюють повну систему несумісних подій. Вихід будемо називати сприятливим для даної події, якщо ця подія здійснюється за такого виходу.

Імовірністю події А (позначатимемо Р(А)) будемо називати відношення кількості сприятливих для події А елементарних виходів, до загальної кількості рівноможливих несумісних елементарних виходів.

Отже, імовірність події А можна обчислити за формулою

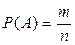, (І.1)

де т ­— кількість сприятливих для події А елементарних виходів, п — загальна кількість можливих елементарних виходів у випробуванні. Тут вважається, що всі виходи є несумісні, рівноможливі і утворюють повну систему.

Приклад 1. В урні міститься три білих і одна чорна кульки. Навмання витягують дві кульки. Знайти імовірність витягання кульок різних кольорів.

Розв’язання: Нехай подія А — витягання двох кульок різних кольорів. Дві кульки з чотирьох можна вибрати 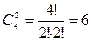способами. Тобто кількість рівноможливих елементарних виходів у випробуванні дорівнює 6. Кількість сприятливих для події А виходів дорівнює 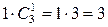. Отже, ймовірність події А дорівнює .

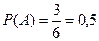Приклад 2. Дитина, яка не вміє читати, складає в ряд кубики з буквами Д, І та Л. Яка ймовірність, що вона утворить слово?

Розв’язання: Нехай подія С — утворення слова. Можливі складання утворюють множину { ДІЛ, ДЛІ, ІЛД, ІДЛ, ЛІД, ЛДІ }, яка містить 6 елементів. Сприятливими для події С будуть складання ДІЛ та ЛІД. Отже, .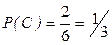

Сформульоване означення називають класичним означенням імовірності.

На основі даного означення можна сформулювати такі властивості імовірності.

1°. Імовірність достеменної події дорівнює 1. ()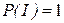

2°. Імовірність неможливої події дорівнює 0. ()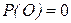

3°. Імовірність випадкової події є додатне число менше, ніж 1. ()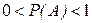

Класичне означення ймовірності передбачає, що кількість елементарних виходів у випробуванні скінчене. Однак на практиці часто зустрічаються випробування з нескінченою кількістю елементарних виходів. Крім того дуже часто неможливо подати результат випробування як сукупність елементарних виходів, а тим більше обґрунтувати їх рівноможливість. Це вказує обмеженість класичного означення імовірності. Подолати цей недолік дозволяє аксіоматичне означення імовірності.

Множину всіх елементарних виходів при даному випробуванні будемо називати простором елементарних подій і позначатимемо Ω. Кожний з елементарних виходів називатимемо точкою простору Ω і позначатимемо ω. Будь-яка подія являтиме собою деяку множину елементарних подій (точок простору Ω). Неможлива подія є порожньою множиною Æ 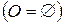. Достеменна подія збігається з простором Ω 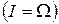. Сумою або об’єднанням двох подій А і В (позначатимемо А + В або 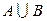) будемо називати подію, яка полягає у здійсненні хоча б однієї з подій А чи В. Добутком або перетином двох подій А і В (позначатимемо А × В або 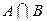) будемо називати подію, яка полягає у здійсненні одночасно обох подій А і В. Протилежною до події А (позначатимемо 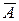) будемо називати подію, яка полягає у нездійсненні події А. Очевидно, 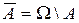. Справджуються рівності: , , , , , , , , , , , , , , .

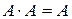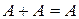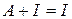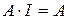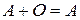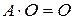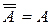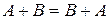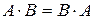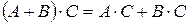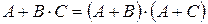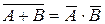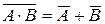Множину подій, для яких визначатимемо імовірності будемо називати полем подій і позначати S. Поле подій S має володіти такими властивостями:

1°. 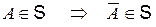, тобто разом з кожною подією А поле подій містить протилежну до неї подію.

2°. 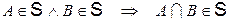, тобто разом з будь-якими двома подіями поле подій містить їх перетин.

3°. 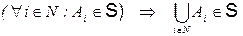, тобто будь-яке злічене об’єднання множин з поля подій також належить цьому полю.

У цьому випадку кажуть, що S є борелівським полем подій або σ- ал­ге­брою подій. Імовірність подій на σ-алгебрі S вводимо таким чином.

Дата добавления: 2015-05-23