
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула повної ймовірності
|
|
|
|
Зауважимо, що на σ-алгебрі S сумі подій А і В відповідає об’єднання множин А і В. Тому, якщо події А і В несумісні, то
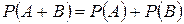 . (І.2)
. (І.2)
Оскільки події А і  несумісні і
несумісні і 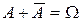 , то
, то 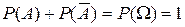 і
і
 . (І.3)
. (І.3)
Якщо події  утворюють повну систему несумісних подій, то
утворюють повну систему несумісних подій, то 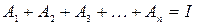 і
і
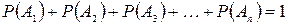 . (І.4)
. (І.4)
Якщо при знаходженні ймовірності події у випробуванні ніяких додаткових умов, крім умов самого випробування, не накладається, то знайдена ймовірність називається безумовною. Якщо накладаються додаткові умови, то знайдену ймовірність називають умовною.
Умовною ймовірністю  називають імовірність події В, знайдену в припущенні, що подія А здійснилася. Умовна ймовірність
називають імовірність події В, знайдену в припущенні, що подія А здійснилася. Умовна ймовірність  дорівнює відношенню ймовірності добутку подій А і В до ймовірності події А, тобто
дорівнює відношенню ймовірності добутку подій А і В до ймовірності події А, тобто
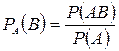 . (І.5)
. (І.5)
Приклад 3. В урні є 5 білих і 4 чорних кульки. З неї послідовно без повернення виймають дві кульки. Знайти ймовірність, що друга кулька виявилась білою, якщо: а) перша кулька була білою? б) перша кулька була чорною?
Розв’язання: Введемо позначення: А — перша кулька була білою; В — перша кулька була чорною; С — друга кулька виявиться білою.
а) Якщо перша кулька виявилась білою, то в урні залишилось 4 білих і 4 чорних кульки. Тому ймовірність, що друга кулька виявиться білою дорівнює 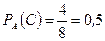 .
.
б) Якщо перша кулька виявилась чорною, то в урні залишилось 5 білих і 3 чорних кульки. Тому ймовірність, що друга кулька виявиться білою дорівнює  .
.
З другого боку ймовірність, що перша кулька виявилась білою дорівнює 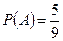 . Знайдемо ймовірність
. Знайдемо ймовірність 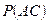 . Всеможливих послідовних виборів двох кульок є 9 × 8 = 72. Сприятливих для АС несумісних рівноможливих виходів є 5 × 4 = 20. Тому
. Всеможливих послідовних виборів двох кульок є 9 × 8 = 72. Сприятливих для АС несумісних рівноможливих виходів є 5 × 4 = 20. Тому  .
.  . Аналогічно
. Аналогічно  ,
, 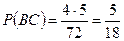 і
і 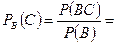
 . Як бачимо результат не залежить від того, чи умовна ймовірність обчислюється безпосередньо, чи на основі формули (І.5).
. Як бачимо результат не залежить від того, чи умовна ймовірність обчислюється безпосередньо, чи на основі формули (І.5).
З формули (І.5) безпосередньо випливає формула для обчислення ймовірності добутку двох подій.
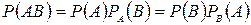 (І.6)
(І.6)
Дві події А і В називаються незалежними, якщо ймовірність однієї з них не залежить від того, чи інша подія відбулась, тобто 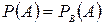 чи
чи 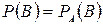 . Очевидно, для незалежних подій справджується формула
. Очевидно, для незалежних подій справджується формула
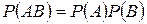 . (І.7)
. (І.7)
Можна сказати, що дві події незалежні, якщо ймовірність їх добутку дорівнює добутку їх імовірностей.
Для довільних подій А і В справджується формула
 . (І.8)
. (І.8)
Дійсно, 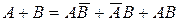 . Тут події
. Тут події  несумісні, тому
несумісні, тому  . Але
. Але 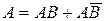 , де
, де  і
і 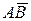 — несумісні, тому
— несумісні, тому  . Так само
. Так само 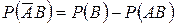 . Тоді
. Тоді 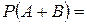
 .
.
Приклад 4. Два стрільці одночасно стріляють по одній мішені. Яка ймовірність попадання в мішень хоча б одним стрільцем, якщо ймовірність попадання в мішень першим стрільцем дорівнює 0,6, а другим — 0,65?
Розв’язання: Введемо позначення: А — попадання в мішень першим стрільцем, В — попадання в мішень другим стрільцем. Тоді  ,
, 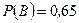 . Оскільки попадання у мішень кожним із стрільців події незалежні, то
. Оскільки попадання у мішень кожним із стрільців події незалежні, то  . Шукана ймовірність дорівнює
. Шукана ймовірність дорівнює 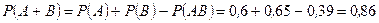 .
.
Нехай подія А може здійснитись за умови здійснення однієї з несумісних подій  , які утворюють повну систему. Тоді здійснення події А означатиме здійснення однієї з несумісних подій
, які утворюють повну систему. Тоді здійснення події А означатиме здійснення однієї з несумісних подій 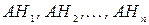 . Отже,
. Отже, 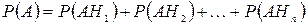 . Але
. Але 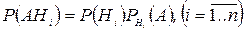 і тому
і тому
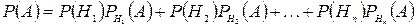 . (І.9)
. (І.9)
Формула (І.9) носить назву формули повної ймовірності.
Приклад 5. Агентство із страхування цивільної відповідальності водіїв розділяє їх на три групи: група тих, що практично не ризикують, група тих, що іноді ризикують і група тих, що дуже часто ризикують. Агентство вважає, що з усіх водіїв, які застрахували автомобілі, 30% належить до першої групи, 50% — до другої групи і 20% — до третьої. Ймовірність того, що протягом року водій з першої групи хоча б один раз потрапить в аварію, складає 0,01, для водія з другої групи — 0,02, а для водія з третьої групи - 0,09. Яка ймовірність, що навмання вибраний водій потрапить в аварію протягом року?
Розв’язання: Введемо позначення: А — водій потрапить в аварію протягом року, Н 1 — водій належить до першої групи, Н 2 — водій належить до другої групи, Н 3 — водій належить до третьої групи. Тоді 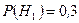 ,
, 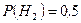 ,
,  ,
,  ,
,  ,
, 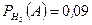 . За формулою повної ймовірності
. За формулою повної ймовірності
 .
.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 411; Нарушение авторских прав?; Мы поможем в написании вашей работы!