Щільність розподілу неперервно розподіленої випадкової величини

Якщо випадкова величина розподілена неперервно, то кількість значень, яких вона може набувати нескінченна, а імовірність, з якою вона набуває кожного конкретного значення, дорівнює нулю. На відміну від дискретно розподіленої випадкової величини така ймовірність не характеризує розподіл величини неперервної. Проте кожному значенню аргументу х можна поставити у відповідність число , яке описує кожну точку х границею відношення імовірності попадання значень випадкової величини Х в деякий окіл цієї точки до величини цього околу. Якщо врахувати, що

,

то щільністю розподілу f (x) неперервної випадкової величини Х будемо називати похідну її функції розподілу:

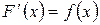(ІІ.3)

Щільність розподілу неперервної випадкової величини має такі властивості:

1. Щільність розподілу завжди невід’ємна ().

Дійсно, оскільки функція розподілу монотонно неспадна, то її похідна в жодній точці не може бути від’ємною.

2. Функція розподілу неперервної випадкової величини визначається через щільність її розподілу за формулою

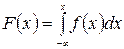(ІІ.4)

Формулу (ІІ.4) отримуємо, проінтегрувавши рівність (ІІ.3) по проміжку .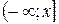

3. Має місце умова нормування

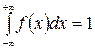(ІІ.5)

На підставі (ІІ.4)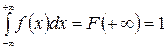

4. Імовірність попадання значень неперервної випадкової величини в заданий інтервал обчислюється за формулою

. (ІІ.6)

Дійсно, .

Приклад 5. Функція розподілу випадкової величини 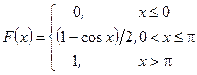. Знайти щільність розподілу та побудувати графіки функції розподілу та щільності розподілу.

Розв’язання: Продиференціювавши вираз для функції розподілу, знаходимо щільність розподілу заданої випадкової величини . Як бачимо, випадкова величина може набувати значень лише з проміжку 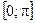. Графіки функції розподілу та щільності розподілу будуємо, використовуючи пакет Maple. Введемо команди

f:=x->piecewise(x<0,0,x>0 and x<Pi,sin(x)/2,x>Pi,0);

F:=x->piecewise(x<0,0,x>0 and x<Pi,(1-cos(x))/2,x>Pi,1);

with(plots):plot([f(x),F(x)],x=-4..4);

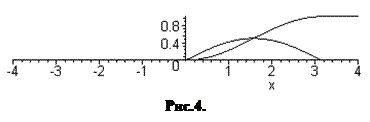і отримаємо шукані графіки (рис.4).

Приклад 6. Щільність розподілу випадкової величини Х задана співвідношенням 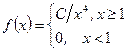. Визначити сталу С та знайти імовірність попадання випадкової величини в проміжок [0; 4].

Розв’язання: Оскільки , то 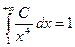, , , С = 3. Отже, 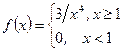. Далі, .

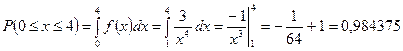Дата добавления: 2015-05-23